平面直角坐标系中 $xOy$ 中,$P$ 是不在 $x$ 轴上的一个动点,过 $P$ 作抛物线 $y^2=4x$ 的两条切线,切点设为 $A,B$,且直线 $PO\perp AB$ 于 $Q$,$R$ 为直线 $AB$ 与 $x$ 轴的交点.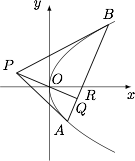

【难度】
【出处】
2014年全国高中数学联赛(一试)
【标注】
-
求证:$R$ 是定点;标注答案定点 $R(2,0)$解析设 $P(m,n)$,则 $AB:ny=2(x+m)$,根据题意,直线 $PO$ 与直线 $AB$ 垂直,于是\[\dfrac nm\cdot \dfrac 2n=-1,\]因此 $m=-2$.进而 $R(2,0)$ 为定点.
-
求 $\dfrac{PQ}{QR}$ 的最小值.标注答案$2\sqrt 2$解析因为 $m=-2$,所以直线 $PO$ 的斜率 $k_{1}=-\dfrac n2$,直线 $PR$ 的斜率 $k_{2}=-\dfrac n4$.
设 $\angle OPR=\alpha$,则 $\alpha$ 为锐角,且\[\begin{split}\dfrac {PQ}{QR}&=\dfrac {1}{\tan \alpha}=\left|\dfrac {1+k_1k_2}{k_1-k_2}\right|\\&=\dfrac {8+n^2}{2|n|}\geqslant \dfrac {2\sqrt {8\cdot n^2}}{2|n|}\\&=2\sqrt 2,\end{split}\]当 $n=\pm 2\sqrt 2$ 时,$\dfrac {PQ}{QR}$ 取到最小值,为 $2\sqrt 2$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2