直线 $l_1,l_2$ 分别是函数 $f(x)=\sin x,x\in [0,\pi]$ 上 $A,B$ 两点处的切线,且 $l_1\perp l_2$.求 $l_1,l_2$ 与 $y$ 轴围成的三角形的面积.
【难度】
【出处】
无
【标注】
【答案】
$\dfrac 14\pi^2$
【解析】
不妨设 $A$ 的横坐标小于 $B$ 的横坐标.由于函数 $f(x)$ 的导函数\[f'(x)=\cos x,\]其值域为 $[-1,1]$.于是 $A,B$ 的横坐标分别为 $0,\pi$.因此 $l_1:y=x$,$l_2:y=-x+\pi$.因此所求的三角形面积为 $\dfrac 14\pi^2$.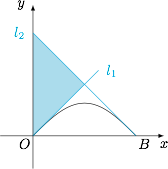

答案
解析
备注