如图,三棱锥 $P-ABC$ 中,平面 $PAC\perp $ 平面 $ABC$,$\angle ABC=\dfrac{\pi}2$,点 $D,E$ 在线段 $AC$ 上,且 $AD=DE=EC=2$,$PD=PC=4$,点 $F$ 在线段 $AB$ 上,且 $EF\parallel BC$.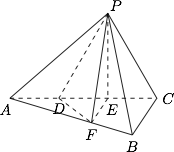

【难度】
【出处】
2015年高考重庆卷(文)
【标注】
-
证明:$AB\perp$ 平面 $PFE$;标注答案略解析在 $\triangle PCD$ 中,$PD=PC$,$DE=EC$,于是 $PE\perp CD$.
又平面 $PAC \perp$ 平面 $ABC$,且两平面的交线为 $AC$,于是 $PE\perp$ 平面 $ABC$,进而 $PE\perp AB$.
在 $\triangle ABC$ 中,$EF\parallel BC$,而 $AB\perp BC$,因此 $AB\perp EF$.
综上,$AB$ 垂直于平面 $PFE$ 中的两条相交直线 $PE$ 和 $EF$,因此 $AB\perp $ 平面 $PEF$. -
若四棱锥 $P-DFBC$ 的体积为 $7$,求线段 $BC$ 的长.标注答案$3$ 或 $3\sqrt 3$解析根据第 $(1)$ 小题的结论,线段 $PE$ 是四棱锥 $P-DFBC$ 的高,且 $PE=2\sqrt 3$,因此由四棱锥 $P-DFBC$ 的体积为 $7$ 可得底面 $DFBC$ 的面积为 $\dfrac{7\sqrt 3}2$.
在底面 $ABC$ 上有$$S_{\triangle FAD}=S_{\triangle FDE},\dfrac{S_{\triangle AEF}}{S_{\triangle ABC}}=\left(\dfrac {AE}{AC}\right)^2=\dfrac 49,$$于是$$\dfrac{S_{DFBC}}{S_{\triangle ABC}}=\dfrac 79,$$因此 $\triangle ABC$ 的面积为 $\dfrac{9\sqrt 3}2$.
这样我们就得到了方程$$\dfrac 12BC\cdot\sqrt{AC^2-BC^2}=\dfrac{9\sqrt 3}2,$$解得 $BC=3$ 或 $BC=3\sqrt 3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2