定义 $f_M(x)=\begin{cases}-1,&x\in M,\\ 1, & x\notin M,\end{cases}$ 且 $M\Delta N=\{x\mid f_M(x)\cdot f_N(x)=-1\}$．集合 $A=\{x \mid x=k,k\in\mathbb N,1\leqslant k\leqslant 2016\}$，集合 $B=\{x\mid x=2k,k\in\mathbb N,1\leqslant k\leqslant 2016\}$．
【难度】
【出处】
2016年清华大学夏令营数学试题
【标注】
-
求 $f_A(2016)$，$f_B(2016)$；标注答案$f_A(2016)=-1$，$f_B(2016)=-1$解析根据 $f_M(x)$ 的定义，有 $f_A(2016)=-1$，$f_B(2016)=-1$．
-
设 ${\rm Card}(X)$ 为集合 $X$ 的元素个数，求 $m={\rm Card}(X\Delta A)+{\rm Card}(X\Delta B)$ 的最小值．标注答案$2016$解析设集合 $X$ 中有 $x_0$ 个元素既不在 $A$ 中也不在 $B$ 中，$x_1$ 个元素只在集合 $A$ 中，$x_2$ 个元素只在集合 $B$ 中，$x_3$ 个元素同时在集合 $A,B$ 中，如图，
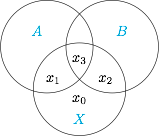则\[\begin{split}m&={\rm Card}(X\Delta A)+{\rm Card}(X\Delta B)\\
&=x_0+x_2+({\rm Card}(A)-x_1-x_3)+x_0+x_1+({\rm Card}(B)-x_2-x_3)\\
&={\rm Card}(A)+{\rm Card}(B)+2x_0-2x_3\\
&\geqslant {\rm Card}(A)+{\rm Card}(B)-2{\rm Card}(A\cap B)\\
&=2016+2016-2\cdot 1008\\
&=2016,\end{split}\]当 $x_0=0,x_3={\rm Card}(A\cap B)$ 时等号成立，即 $A\cap B\subseteq X$，且 $X\subseteq(A\cup B)$ 时可取到最小值，也可以直接取 $X=A\cap B$．因此所求的最小值为 $2016$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
