如图,在等腰 $\triangle ABC$ 中,已知 $A=100^\circ$,$B$ 的角平分线交 $AC$ 于 $D$,求证:$AD+DB=BC$.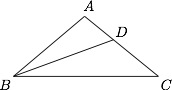

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
 则 $\triangle ABD$ 与 $\triangle EBD$ 全等,从而有$$AD=DE,\angle DEB=100^\circ.$$又因为$$ \angle DFB=\angle BDF=80^\circ=\angle DEF,$$所以 $ \angle DCB=40^\circ=\angle CDF $,从而有 $ DE=DF=AD=CF $,所以 $ BC=BF+FC=DB+AD$.
则 $\triangle ABD$ 与 $\triangle EBD$ 全等,从而有$$AD=DE,\angle DEB=100^\circ.$$又因为$$ \angle DFB=\angle BDF=80^\circ=\angle DEF,$$所以 $ \angle DCB=40^\circ=\angle CDF $,从而有 $ DE=DF=AD=CF $,所以 $ BC=BF+FC=DB+AD$.
答案
解析
备注