查看数据源：59083050060a050008e62230
求函数 $f(x)=\cos x+\sqrt{\cos^2x-4\sqrt{2}\cos x+4\sin x+9}$ 的最大值与最小值．
【难度】
【出处】
无
【标注】
  • 方法
    >
    数形结合
    >
    转化为距离
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的定义
    >
    椭圆的焦准定义
【答案】
$\sqrt 5+\sqrt 2$，$\sqrt{13}-\sqrt 2$
【解析】
首先对函数 $f(x)$ 进行代数变形，以期挖掘几何意义：$$f(x)=\cos x+\sqrt{\left(\sqrt 2\cos x-2\right)^2+\left(\sin x+2\right)^2}.$$根号下的部分的几何意义比较明显，即椭圆 $\dfrac{m^2}2+n^2=1$ 上的点 $P\left(\sqrt 2\cos x,\sin x\right)$ 到点 $A\left(2,-2\right)$ 的距离，那么剩下的 $\cos x$ 的几何意义是什么呢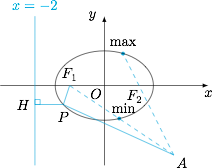？注意到椭圆的左准线为 $x=-2$，离心率 $e=\dfrac{\sqrt 2}2$，于是 $P$ 到左焦点的距离为$$PF_1=\dfrac{\sqrt 2}2\left(\sqrt 2\cos x+2\right)=\cos x+\sqrt 2.$$因此我们有$$f(x)=PF_1+PA-\sqrt 2\geqslant F_1A-\sqrt 2=\sqrt{13}-\sqrt 2.$$另一方面，由椭圆的定义，有$$f(x)=\left(2\sqrt 2-PF_2\right)+PA-\sqrt 2=PA-PF_2+\sqrt 2\leqslant AF_2+\sqrt 2=\sqrt 5+\sqrt 2,$$于是函数的最大值与最小值分别为 $\sqrt 5+\sqrt 2$ 和 $\sqrt{13}-\sqrt 2$．
答案 解析 备注
0.108019s