已知 $P$ 为 $\triangle ABC$ 内一点，求证：$S_A\overrightarrow{PA}+S_B\overrightarrow{PB}+S_C\overrightarrow{PC}=\overrightarrow 0$，其中 $S_{A}$，$S_{B}$，$S_{C}$ 分别是 $\triangle BPC$，$\triangle CPA$，$\triangle APB$ 的面积．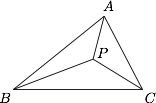
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
延长 $AP$ 交边 $BC$ 于点 $Q$，如图．
由于 $\overrightarrow{AP}=\dfrac{S_{C}+S_{B}}{S_{\triangle ABC}}\overrightarrow{AQ}$，且根据共线向量的表达，有$$\overrightarrow{AQ}=\dfrac{S_{C}}{S_{C}+S_{B}}\overrightarrow{AC}+\dfrac{S_{B}}{S_{C}+S_{B}}\overrightarrow{AB}.$$从而可得$$\overrightarrow{AP}=\dfrac{S_{C}}{S_{\triangle ABC}}\overrightarrow{AC}+\dfrac{S_{B}}{S_{\triangle ABC}}\overrightarrow{AB}.$$对上式应用向量的换底公式（$\overrightarrow{AB}=\overrightarrow{MB}-\overrightarrow{MA}$），将所有的向量改写为以 $P$ 为起点的，$$-\overrightarrow{PA}=\dfrac{S_{C}}{S_{\triangle ABC}}\left(\overrightarrow{PC}-\overrightarrow{PA}\right)+\dfrac{S_{B}}{S_{\triangle ABC}}\left(\overrightarrow{PB}-\overrightarrow{PA}\right),$$整理即得．
由于 $\overrightarrow{AP}=\dfrac{S_{C}+S_{B}}{S_{\triangle ABC}}\overrightarrow{AQ}$，且根据共线向量的表达，有$$\overrightarrow{AQ}=\dfrac{S_{C}}{S_{C}+S_{B}}\overrightarrow{AC}+\dfrac{S_{B}}{S_{C}+S_{B}}\overrightarrow{AB}.$$从而可得$$\overrightarrow{AP}=\dfrac{S_{C}}{S_{\triangle ABC}}\overrightarrow{AC}+\dfrac{S_{B}}{S_{\triangle ABC}}\overrightarrow{AB}.$$对上式应用向量的换底公式（$\overrightarrow{AB}=\overrightarrow{MB}-\overrightarrow{MA}$），将所有的向量改写为以 $P$ 为起点的，$$-\overrightarrow{PA}=\dfrac{S_{C}}{S_{\triangle ABC}}\left(\overrightarrow{PC}-\overrightarrow{PA}\right)+\dfrac{S_{B}}{S_{\triangle ABC}}\left(\overrightarrow{PB}-\overrightarrow{PA}\right),$$整理即得．
答案
解析
备注
