在 $\triangle ABC$ 中,角 $A,B,C$ 所对的边分别为 $a,b,c$,已知 $O,G,I$ 分别为 $\triangle ABC$ 的外心、重心、内心,且 $AG\perp OI$,求证:$\dfrac 1b+\dfrac 1c=\dfrac 2a$.
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
由题意知$$\overrightarrow{AG}\cdot\overrightarrow{OI}=\dfrac 13(\overrightarrow{AB}+\overrightarrow{AC})\cdot(\overrightarrow{AI}-\overrightarrow{AO})=0,$$而\[\begin{split} &(\overrightarrow{AB}+\overrightarrow{AC})\cdot(\overrightarrow{AI}-\overrightarrow{AO})\\
=&(\overrightarrow{AB}+\overrightarrow{AC})\cdot\left(\dfrac b{a+b+c}\overrightarrow{AB}+\dfrac c{a+b+c}\overrightarrow{AC}-\overrightarrow{AO}\right)\\
=&\dfrac {bc^2+cb^2}{a+b+c}+\dfrac {b+c}{a+b+c}\cdot bc\cdot\dfrac {b^2+c^2-a^2}{2bc}-\dfrac 12c^2-\dfrac 12b^2\\
=&\dfrac 12(2bc-ab-ac)=0.\end{split}\]从而有$$\dfrac 2a=\dfrac 1b+\dfrac 1c.$$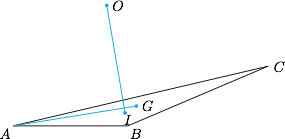
=&(\overrightarrow{AB}+\overrightarrow{AC})\cdot\left(\dfrac b{a+b+c}\overrightarrow{AB}+\dfrac c{a+b+c}\overrightarrow{AC}-\overrightarrow{AO}\right)\\
=&\dfrac {bc^2+cb^2}{a+b+c}+\dfrac {b+c}{a+b+c}\cdot bc\cdot\dfrac {b^2+c^2-a^2}{2bc}-\dfrac 12c^2-\dfrac 12b^2\\
=&\dfrac 12(2bc-ab-ac)=0.\end{split}\]从而有$$\dfrac 2a=\dfrac 1b+\dfrac 1c.$$

答案
解析
备注