如图，已知扇形 $AOB$ 的圆心角为 $120^\circ$，$P$ 为弧 $AB$ 上一点，$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$．求 $x+y$ 的取值范围．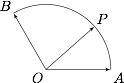
【难度】
【出处】
无
【标注】
【答案】
$[1,2]$
【解析】
连接 $AB$，作弧 $AB$ 的切线 $l$ 使得 $l\parallel AB$，设切点为 $M$．连接 $OM$ 交 $AB$ 于 $N$．
我们熟知，若点 $P$ 落在直线 $AB$ 上，则 $x+y=1$．而由已知条件不难推知 $OM=2ON$，于是若点 $P$ 落在切线 $l$ 上，则 $x+y=2$．事实上，弧 $AB$ 落在直线 $AB$ 和切线 $l$ 之间，于是 $x+y$ 的取值范围是 $[1,2]$．
我们熟知，若点 $P$ 落在直线 $AB$ 上，则 $x+y=1$．而由已知条件不难推知 $OM=2ON$，于是若点 $P$ 落在切线 $l$ 上，则 $x+y=2$．事实上，弧 $AB$ 落在直线 $AB$ 和切线 $l$ 之间，于是 $x+y$ 的取值范围是 $[1,2]$．
答案
解析
备注
