已知数列 $\{a_n\}$ 是公差为 $d$,首项 $a_1=1$ 的等差数列,问是否存在实数 $d$ 使得数列 $\left\{\dfrac{1}{a_n}\right\}$ 满足:可以从中取出无限多项,并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的 $d$ 的值;若不存在,说明理由.
【难度】
【出处】
无
【标注】
【答案】
满足条件的 $d$ 只有一个,为 $0$
【解析】
满足条件的 $d$ 只有一个,为 $0$.当 $d=0$ 时,显然符合题意,接下来按 $d$ 的正负讨论,如图.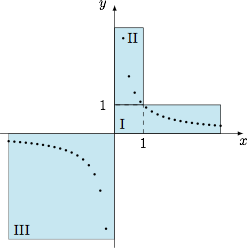
情形一 $d>0$.
此时 $\left\{\dfrac{1}{a_n}\right\}$ 的子列在区域I中,于是数列 $\left\{\dfrac{1}{a_n}\right\}$ 有下界 $0$.考虑到 $\left\{\dfrac{1}{a_n}\right\}$ 的子列按原有的先后次序排列,若能组成等差数列,从区域I中自左向右取项时公差为负数,该数列一定没有下界,矛盾.
情形二 $d<0$.
此时 $\left\{\dfrac{1}{a_n}\right\}$ 的子列在区域II及区域III中.考虑到 $\left\{\dfrac{1}{a_n}\right\}$ 的子列按原有的先后次序排列,因此不可能同时包含区域II及区域III中的项.区域II中的项数有限,而按自右往左在区域III中取项时,公差为正数,与有上界矛盾.
综上,满足条件的 $d$ 只有一个,为 $0$.

此时 $\left\{\dfrac{1}{a_n}\right\}$ 的子列在区域I中,于是数列 $\left\{\dfrac{1}{a_n}\right\}$ 有下界 $0$.考虑到 $\left\{\dfrac{1}{a_n}\right\}$ 的子列按原有的先后次序排列,若能组成等差数列,从区域I中自左向右取项时公差为负数,该数列一定没有下界,矛盾.
此时 $\left\{\dfrac{1}{a_n}\right\}$ 的子列在区域II及区域III中.考虑到 $\left\{\dfrac{1}{a_n}\right\}$ 的子列按原有的先后次序排列,因此不可能同时包含区域II及区域III中的项.区域II中的项数有限,而按自右往左在区域III中取项时,公差为正数,与有上界矛盾.
综上,满足条件的 $d$ 只有一个,为 $0$.
答案
解析
备注