解不等式：$\sqrt{x^2+4x+8}+\sqrt{x^2-4x+8}\leqslant 6$．
【难度】
【出处】
无
【标注】
【答案】
$\left[-\dfrac 3{\sqrt 5},\dfrac{3}{\sqrt 5}\right]$
【解析】
原不等式即$$\sqrt{(x+2)^2+(2-0)^2}+\sqrt{(x-2)^2+(2-0)^2}\leqslant 6.$$联想椭圆的定义，构造以 $F_1(-2,0),F_2(2,0)$ 为焦点，$6$ 为长轴长的椭圆 $\dfrac{x^2}{9}+\dfrac{y^2}{5}=1$．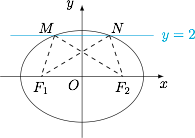
于是所求 $x$ 的范围即直线 $y=2$ 被椭圆截得的弦 $MN$ 上的点的横坐标的取值范围，即 $\left[-\dfrac 3{\sqrt 5},\dfrac{3}{\sqrt 5}\right]$．
于是所求 $x$ 的范围即直线 $y=2$ 被椭圆截得的弦 $MN$ 上的点的横坐标的取值范围，即 $\left[-\dfrac 3{\sqrt 5},\dfrac{3}{\sqrt 5}\right]$．
答案
解析
备注
