已知 $a>0$，$a^2-2ab+c^2=0$，$bc>a^2$，试比较 $a,b,c$ 的大小．
【难度】
【出处】
无
【标注】
【答案】
$b>c>a$
【解析】
根据题意，有$$\begin{cases}1-2\cdot\dfrac ba+\left(\dfrac ca\right)^2=0\\\dfrac ba\cdot\dfrac ca>1\end{cases}$$令 $\dfrac ba=x$，$\dfrac ca=y$，则$$\begin{cases} y^2-2x+1=0,\\ xy>1.\end{cases}$$由于 $b=\dfrac{a^2+c^2}{2a}>0$，由 $bc>a^2>0$，于是 $x,y>0$，因此$$\begin{cases} y= \sqrt{2x-1},\\ y>\dfrac 1x,\end{cases}$$如图作出可行域．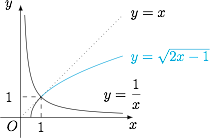
由图可得 $x>y>1$，于是 $b>c>a$．
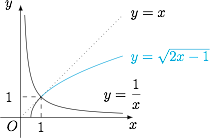由图可得 $x>y>1$，于是 $b>c>a$．
答案
解析
备注
