已知圆 $A:x^2+y^2-6y+m=0$ 和直线 $l:x+2y-3=0$ 交于 $P,Q$ 两点，且以 $PQ$ 为直径的圆 $M$ 过原点，求 $m$ 的值．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{18}5$
【解析】
画出示意图如下．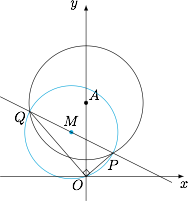
取圆 $A$ 与直线 $l$ 的交点曲线系$$\Gamma (\lambda):x^2+y^2-6y+m+\lambda\left(x+2y-3\right)=0,$$其中 $\lambda$ 为参数．整理上述方程，得$$\Gamma (\lambda):\left(x+\dfrac{\lambda}{2}\right)^2+\left(y-3+\lambda\right)^2+m-3\lambda-\dfrac 14\lambda^2-\left(3-\lambda\right)^2=0.$$我们想使 $\Gamma (\lambda)$ 表示以 $PQ$ 为直径的圆，只需要圆心在直线 $x+2y-3=0$ 上，因此$$-\dfrac{\lambda}{2}+2\cdot\left(3-\lambda\right)-3=0,$$解得 $\lambda=\dfrac 65$．又圆 $\Gamma\left(\dfrac 65\right)$ 经过原点 $(0,0)$，所以$$m-3\lambda=0,$$进而可得 $m=\dfrac{18}5$．
取圆 $A$ 与直线 $l$ 的交点曲线系$$\Gamma (\lambda):x^2+y^2-6y+m+\lambda\left(x+2y-3\right)=0,$$其中 $\lambda$ 为参数．整理上述方程，得$$\Gamma (\lambda):\left(x+\dfrac{\lambda}{2}\right)^2+\left(y-3+\lambda\right)^2+m-3\lambda-\dfrac 14\lambda^2-\left(3-\lambda\right)^2=0.$$我们想使 $\Gamma (\lambda)$ 表示以 $PQ$ 为直径的圆，只需要圆心在直线 $x+2y-3=0$ 上，因此$$-\dfrac{\lambda}{2}+2\cdot\left(3-\lambda\right)-3=0,$$解得 $\lambda=\dfrac 65$．又圆 $\Gamma\left(\dfrac 65\right)$ 经过原点 $(0,0)$，所以$$m-3\lambda=0,$$进而可得 $m=\dfrac{18}5$．
答案
解析
备注
