如图，正方体 $ABCD-A_1B_1C_1D_1$ 的棱长为 $a$，动点 $P$ 在对角线 $BD_1$ 上，过 $P$ 作垂直于 $BD_1$ 的平面 $\alpha$，记这样得到的截面多边形（含三角形）的周长为 $L$，面积为 $S$，$BP=x$，作出函数 $L(x)$ 与 $S(x)$ 的图象．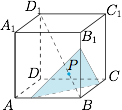
【难度】
【出处】
无
【标注】
【答案】
曲线如图：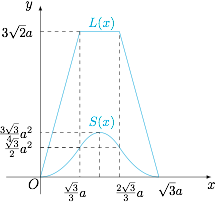
【解析】
为了看清楚截面，我们作沿着正方体 $ABCD-A_1B_1C_1D_1$ 的体对角线 $BD_1$ 方向的正投影，并将截面三角形的变化过程绘图如下：
运动的三个阶段可以借助下面两个图帮助想象（$B\to P\to Q\to D_1$ 的三等分线段与 $B\to A\to D\to B$ 的等边三角形分别对应）：
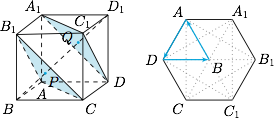其中第二阶段（六边形阶段）最为复杂，依靠下图可以证明此阶段周长为定值，而面积不为定值（服从二次函数关系）．
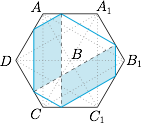最后整理出所求的曲线如图：其中$$L(x)=\begin{cases}3\sqrt 6 x,&x\in\left[0,\dfrac{\sqrt 3}3a\right),\\ 3\sqrt 2a,&x\in\left[\dfrac{\sqrt 3}3a,\dfrac{2\sqrt 3}3a\right],\\ 9\sqrt 2a-3\sqrt 6 x,&x\in\left(\dfrac{2\sqrt 3}3a,\sqrt 3a\right],\end{cases}$$而$$S(x)=\begin{cases} \dfrac{3\sqrt 3}2x^2,&x\in\left[0,\dfrac{\sqrt 3}3a\right),\\ -3\sqrt 3\left(x-\dfrac{\sqrt 3}2a\right)^2+\dfrac{3\sqrt 3}4a^2,&x\in\left[\dfrac{\sqrt 3}3a,\dfrac{2\sqrt 3}3a\right],\\ \dfrac{3\sqrt 3}2\left(x-\sqrt 3a\right)^2,&x\in\left(\dfrac{2\sqrt 3}3a,\sqrt 3a\right],\end{cases}$$
运动的三个阶段可以借助下面两个图帮助想象（$B\to P\to Q\to D_1$ 的三等分线段与 $B\to A\to D\to B$ 的等边三角形分别对应）：其中第二阶段（六边形阶段）最为复杂，依靠下图可以证明此阶段周长为定值，而面积不为定值（服从二次函数关系）．最后整理出所求的曲线如图：其中$$L(x)=\begin{cases}3\sqrt 6 x,&x\in\left[0,\dfrac{\sqrt 3}3a\right),\\ 3\sqrt 2a,&x\in\left[\dfrac{\sqrt 3}3a,\dfrac{2\sqrt 3}3a\right],\\ 9\sqrt 2a-3\sqrt 6 x,&x\in\left(\dfrac{2\sqrt 3}3a,\sqrt 3a\right],\end{cases}$$而$$S(x)=\begin{cases} \dfrac{3\sqrt 3}2x^2,&x\in\left[0,\dfrac{\sqrt 3}3a\right),\\ -3\sqrt 3\left(x-\dfrac{\sqrt 3}2a\right)^2+\dfrac{3\sqrt 3}4a^2,&x\in\left[\dfrac{\sqrt 3}3a,\dfrac{2\sqrt 3}3a\right],\\ \dfrac{3\sqrt 3}2\left(x-\sqrt 3a\right)^2,&x\in\left(\dfrac{2\sqrt 3}3a,\sqrt 3a\right],\end{cases}$$
答案
解析
备注
