求抛物线 $y^2=2px(p>0)$ 的内接等腰直角三角形面积的最小值．
【难度】
【出处】
无
【标注】
【答案】
$4p^2$
【解析】
设 $A\left(2pa^2,2pa\right),B\left(2pb^2,2pb\right),C\left(2pc^2,2pc\right)$，且 $A$ 为直角顶点，如图．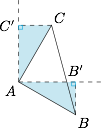
注意到 $\triangle ABB'$ 与 $\triangle ACC'$ 全等，因此 $AB'=AC'$，等腰直角 $\triangle ABC$ 的面积$$S_{\triangle ABC}=\dfrac 12AB^2=2p^2\left[(a-b)^2+(c-a)^2\right]=2p^2[2a^2-2a(b+c)+b^2+c^2].$$又 $AC\perp AB$，于是$$(2pa^2-2pb^2)(2pa^2-2pc^2)+(2pa-2pb)(2pa-2pc)=0,$$整理得$$(a+b)(a+c)+1=0,$$即$$a^2+bc+1=-a(b+c),$$代入面积的计算式可得$$S_{\triangle ABC}=2p^2\left[4a^2+(b+c)^2+2\right].$$于是抛物线的内接等腰直角三角形面积最小值为 $4p^2$，当 $A(0,0),B(2p,2p),C(2p,-2p)$ 时可以取得．
注意到 $\triangle ABB'$ 与 $\triangle ACC'$ 全等，因此 $AB'=AC'$，等腰直角 $\triangle ABC$ 的面积$$S_{\triangle ABC}=\dfrac 12AB^2=2p^2\left[(a-b)^2+(c-a)^2\right]=2p^2[2a^2-2a(b+c)+b^2+c^2].$$又 $AC\perp AB$，于是$$(2pa^2-2pb^2)(2pa^2-2pc^2)+(2pa-2pb)(2pa-2pc)=0,$$整理得$$(a+b)(a+c)+1=0,$$即$$a^2+bc+1=-a(b+c),$$代入面积的计算式可得$$S_{\triangle ABC}=2p^2\left[4a^2+(b+c)^2+2\right].$$于是抛物线的内接等腰直角三角形面积最小值为 $4p^2$，当 $A(0,0),B(2p,2p),C(2p,-2p)$ 时可以取得．
答案
解析
备注
