证明：从双曲线焦点出发的光线，经过双曲线反射后反射光线的反向延长线必经过另一个焦点．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设双曲线方程为 $\dfrac{{{x^2}}}{{{a^2}}}-\dfrac{{{y^2}}}{{{b^2}}} = 1$，如图．设光线从焦点 $F_1$ 出发，经过双曲线上一点 $A$，$l$ 是过 $A$ 点的双曲线的切线，交 $x$ 轴于 $B$，连接 $A{F_2}$，证明 $AB$ 为 $\angle {F_1}A{F_2}$ 的角平分线即可．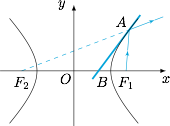
不妨设 $A(p,q)$ 在第一象限，则切线的斜率为 ${k_l}=\dfrac{{p{b^2}}}{{q{a^2}}}$，从而直线 $l$ 的方程为$$y-q=\dfrac {pb^2}{qa^2}(x-p),$$于是可得$$x_B=p-\dfrac {q^2a^2}{pb^2}=p-\dfrac {a^2}{p}\left(\dfrac {p^2}{a^2}-1\right)=\dfrac {a^2}p.$$所以$$\dfrac{|BF_1|}{|BF_2|}=\dfrac{c-\frac{a^2}p}{c+\frac{a^2}p}=\dfrac{cp-a^2}{cp+a^2}.$$设 $A$ 到双曲线的左、右准线的距离分别为 ${h_1},{h_2}$，则$$\dfrac{{|A{F_1}|}}{{|A{F_2}|}} = \dfrac{{{h_1}}}{{{h_2}}} = \dfrac{p-\dfrac{a^2}c}{p+{\dfrac{a^2}c}} = \dfrac{pc-a^2}{pc+a^2}.$$所以有 $\dfrac{|BF_1|}{|BF_2|}=\dfrac{{|A{F_1}|}}{{|A{F_2}|}}$，从而 $AB$ 为 $\angle {F_1}A{F_2}$ 的角平分线，所以反射光线过焦点 $F_2$．
不妨设 $A(p,q)$ 在第一象限，则切线的斜率为 ${k_l}=\dfrac{{p{b^2}}}{{q{a^2}}}$，从而直线 $l$ 的方程为$$y-q=\dfrac {pb^2}{qa^2}(x-p),$$于是可得$$x_B=p-\dfrac {q^2a^2}{pb^2}=p-\dfrac {a^2}{p}\left(\dfrac {p^2}{a^2}-1\right)=\dfrac {a^2}p.$$所以$$\dfrac{|BF_1|}{|BF_2|}=\dfrac{c-\frac{a^2}p}{c+\frac{a^2}p}=\dfrac{cp-a^2}{cp+a^2}.$$设 $A$ 到双曲线的左、右准线的距离分别为 ${h_1},{h_2}$，则$$\dfrac{{|A{F_1}|}}{{|A{F_2}|}} = \dfrac{{{h_1}}}{{{h_2}}} = \dfrac{p-\dfrac{a^2}c}{p+{\dfrac{a^2}c}} = \dfrac{pc-a^2}{pc+a^2}.$$所以有 $\dfrac{|BF_1|}{|BF_2|}=\dfrac{{|A{F_1}|}}{{|A{F_2}|}}$，从而 $AB$ 为 $\angle {F_1}A{F_2}$ 的角平分线，所以反射光线过焦点 $F_2$．
答案
解析
备注
