已知 $A,B$ 是以 $F_1,F_2$ 为焦点的椭圆上(不在长轴上)两点,且 $F_1A\parallel F_2B$.$M$ 为 $F_1B$ 与 $F_2A$ 的交点,求证:$M$ 的轨迹也是以 $F_1,F_2$ 为焦点的椭圆.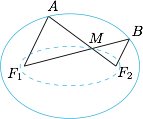

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设 $AF_1=m$,$BF_2=n$,则 $AF_2=2a-m$,$BF_1=2a-n$.由题意$$\dfrac{MF_1}{MB}=\dfrac{MA}{MF_2}=\dfrac{AF_1}{BF_2}=\dfrac mn.$$于是$$MF_1=\dfrac m{m+n}\cdot (2a-n),MF_2=\dfrac n{m+n}\cdot(2a-m).$$因此$$MF_1+MF_2=2a-\dfrac 2{\dfrac 1m+\dfrac 1n}.$$我们熟知$$\dfrac 1m+\dfrac 1n=\dfrac 2{ep},$$其中 $e$ 是椭圆的离心率,$p$ 为椭圆的焦点到对应准线的距离,因此原命题得证.进一步,由于 $ep=\dfrac {b^2}{a}$(即椭圆的半通径长),因此新的椭圆的离心率为$$\dfrac{2c}{2a-\dfrac {b^2}{a}}=\dfrac{2e}{1+e^2}.$$
答案
解析
备注