已知椭圆 $E$ 的离心率为 $\dfrac 13$，左、右焦点分别为 $F_1,F_2$，$P$ 为椭圆左准线上的一点，求 $\tan\angle F_1PF_2$ 的最大值．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {\sqrt 5}{20}$
【解析】
考虑对点 $F_1,F_2$ 所张角为定值的点在圆上，当过点 $F_1F_2$ 的圆与椭圆的准线相切时，$\angle F_1PF_2$ 有最大值，如下图：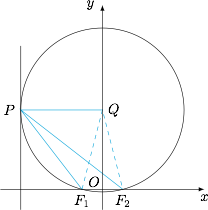
此时对应圆心为 $Q$，有$$\angle F_1PF_2=\angle OQF_1,$$而$$F_1O=c,QF_1=PQ=\dfrac {a^2}{c}=9c,$$所以$$[\tan\angle F_1PF_2]_{\max}=\dfrac {OF_1}{QO}=\dfrac c{\sqrt{81c^2-c^2}}=\dfrac {\sqrt 5}{20}.$$
此时对应圆心为 $Q$，有$$\angle F_1PF_2=\angle OQF_1,$$而$$F_1O=c,QF_1=PQ=\dfrac {a^2}{c}=9c,$$所以$$[\tan\angle F_1PF_2]_{\max}=\dfrac {OF_1}{QO}=\dfrac c{\sqrt{81c^2-c^2}}=\dfrac {\sqrt 5}{20}.$$
答案
解析
备注
