已知 $\triangle ABC$ 中，$AM$ 为 $BC$ 边上的中线（$M$ 在 $BC$ 边上），且满足 $AM=AB-AC$，$BC=4$．求点 $A$ 到直线 $BC$ 距离的最大值．
【难度】
【出处】
无
【标注】
【答案】
$\sqrt 3$
【解析】
如图建系．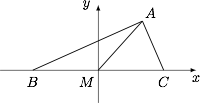
设 $AM=2a$，则 $A$ 点为双曲线 $E:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$（其中 $a^2+b^2=4$）和圆 $F:x^2+y^2=4a^2$ 的交点，于是可得$$\dfrac{y^2}{a^2}+\dfrac{y^2}{b^2}=3,$$进而$$y^2=\dfrac 32\cdot\dfrac{2}{\dfrac 1{a^2}+\dfrac 1{b^2}}\leqslant \dfrac 32\cdot\dfrac {a^2+b^2}2=3,$$等号当且仅当 $a=b=\sqrt 2$ 时取得．因此所求点 $A$ 到直线 $BC$ 的最大距离为 $\sqrt 3$．
设 $AM=2a$，则 $A$ 点为双曲线 $E:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$（其中 $a^2+b^2=4$）和圆 $F:x^2+y^2=4a^2$ 的交点，于是可得$$\dfrac{y^2}{a^2}+\dfrac{y^2}{b^2}=3,$$进而$$y^2=\dfrac 32\cdot\dfrac{2}{\dfrac 1{a^2}+\dfrac 1{b^2}}\leqslant \dfrac 32\cdot\dfrac {a^2+b^2}2=3,$$等号当且仅当 $a=b=\sqrt 2$ 时取得．因此所求点 $A$ 到直线 $BC$ 的最大距离为 $\sqrt 3$．
答案
解析
备注
