设封闭曲线 $E_n:\dfrac{x^{2^n}}{a^2}+\dfrac{y^{2^n}}{b^2}=1$（$a,b\geqslant 2$，$n\in\mathbb N^*$）所围成的面积为 $S_n$，求证：$4<S_n\leqslant ab\pi$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
当 $n=1$ 时，封闭曲线为椭圆$$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1.$$考虑到在仿射变换 $x=ax'$，$y=by'$ 下，该图形即圆$$x'^2+y'^2=1,$$面积为 $\pi$，因此 $S_1=ab\pi$．
下面证明 $\{S_n\}$ 单调递减，只需要证明曲线 $E_n$ 上任意一点均在曲线 $E_{n+1}$ 的外部，也即若 $\dfrac{x^{2^n}}{a^2}+\dfrac{y^{2^n}}{b^2}=1$，则有$$\dfrac{x^{2^{n+1}}}{a^2}+\dfrac{y^{2^{n+1}}}{b^2}>1.$$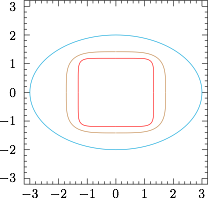
这可以由柯西不等式证明，由于$$1=\dfrac 1a\cdot \dfrac{x^{2^n}}{a}+\dfrac 1b\cdot \dfrac{y^{2^n}}{b}\leqslant\sqrt{\dfrac 1{a^2}+\dfrac 1{b^2}}\cdot\sqrt{\dfrac{x^{2^{n+1}}}{a^2}+\dfrac{y^{2^{n+1}}}{b^2}},$$而$$\sqrt{\dfrac 1{a^2}+\dfrac 1{b^2}}<1,$$于是有$$\sqrt{\dfrac{x^{2^{n+1}}}{a^2}+\dfrac{y^{2^{n+1}}}{b^2}}>1.$$最后证明 $S_n>4$，事实上，对于满足$$-1\leqslant x\leqslant 1,-1\leqslant y\leqslant 1$$的任意一点 $(x,y)$，均有$$\dfrac{x^{2^n}}{a^2}+\dfrac{y^{2^n}}{b^2}\leqslant \dfrac{1}{a^2}+\dfrac{1}{b^2}<1,$$于是以 $(1,1),(1,-1),(-1,-1),(-1,1)$ 为顶点的正方形及其内部的点都在 $E_n$ 内部，于是 $S_n>4$．
事实上，$4$ 是 $\{S_n\}$ 的下确界，证明如下．
将曲线 $E_n$ 的方程变形为$$\left(\dfrac x{a^{\frac 1{2^{n-1}}}}\right)^{2^n}+\left(\dfrac y{b^{\frac 1{2^{n-1}}}}\right)^{2^n}=1,$$作仿射变换 $x=a^{\frac 1{2^{n-1}}}x'$，$y=b^{\frac 1{2^{n-1}}}y'$．设封闭曲线 $F_n$ 的方程为$$x'^{2^n}+y'^{2^n}=1,$$其面积为 $T_n$，则有$$S_n=(ab)^{\frac 1{2^{n-1}}}T_n.$$考虑到$$T_n=4\int_0^1\left(1-x^{2^n}\right)^{\frac 1{2^n}}{\rm d}x,$$而$$\lim_{n\to +\infty}\left(1-x^{2^n}\right)^{\frac 1{2^n}}=1,$$于是$$\lim_{n\to +\infty}T_n=4,$$因此$$\lim_{n\to +\infty}S_n=\lim_{n\to +\infty}(ab)^{\frac 1{2^{n-1}}}\cdot \lim_{n\to +\infty}T_n=4.$$
下面证明 $\{S_n\}$ 单调递减，只需要证明曲线 $E_n$ 上任意一点均在曲线 $E_{n+1}$ 的外部，也即若 $\dfrac{x^{2^n}}{a^2}+\dfrac{y^{2^n}}{b^2}=1$，则有$$\dfrac{x^{2^{n+1}}}{a^2}+\dfrac{y^{2^{n+1}}}{b^2}>1.$$
这可以由柯西不等式证明，由于$$1=\dfrac 1a\cdot \dfrac{x^{2^n}}{a}+\dfrac 1b\cdot \dfrac{y^{2^n}}{b}\leqslant\sqrt{\dfrac 1{a^2}+\dfrac 1{b^2}}\cdot\sqrt{\dfrac{x^{2^{n+1}}}{a^2}+\dfrac{y^{2^{n+1}}}{b^2}},$$而$$\sqrt{\dfrac 1{a^2}+\dfrac 1{b^2}}<1,$$于是有$$\sqrt{\dfrac{x^{2^{n+1}}}{a^2}+\dfrac{y^{2^{n+1}}}{b^2}}>1.$$最后证明 $S_n>4$，事实上，对于满足$$-1\leqslant x\leqslant 1,-1\leqslant y\leqslant 1$$的任意一点 $(x,y)$，均有$$\dfrac{x^{2^n}}{a^2}+\dfrac{y^{2^n}}{b^2}\leqslant \dfrac{1}{a^2}+\dfrac{1}{b^2}<1,$$于是以 $(1,1),(1,-1),(-1,-1),(-1,1)$ 为顶点的正方形及其内部的点都在 $E_n$ 内部，于是 $S_n>4$．事实上，$4$ 是 $\{S_n\}$ 的下确界，证明如下．
将曲线 $E_n$ 的方程变形为$$\left(\dfrac x{a^{\frac 1{2^{n-1}}}}\right)^{2^n}+\left(\dfrac y{b^{\frac 1{2^{n-1}}}}\right)^{2^n}=1,$$作仿射变换 $x=a^{\frac 1{2^{n-1}}}x'$，$y=b^{\frac 1{2^{n-1}}}y'$．设封闭曲线 $F_n$ 的方程为$$x'^{2^n}+y'^{2^n}=1,$$其面积为 $T_n$，则有$$S_n=(ab)^{\frac 1{2^{n-1}}}T_n.$$考虑到$$T_n=4\int_0^1\left(1-x^{2^n}\right)^{\frac 1{2^n}}{\rm d}x,$$而$$\lim_{n\to +\infty}\left(1-x^{2^n}\right)^{\frac 1{2^n}}=1,$$于是$$\lim_{n\to +\infty}T_n=4,$$因此$$\lim_{n\to +\infty}S_n=\lim_{n\to +\infty}(ab)^{\frac 1{2^{n-1}}}\cdot \lim_{n\to +\infty}T_n=4.$$
答案
解析
备注
