已知 $f(x)=ax^2+|x-a|+b$,若对于任意 $b\in [0,1]$ 和任意 $x\in [-3,3]$ 均有 $|f(x)|\leqslant 2$ 恒成立,求 $a$ 的取值范围.
【难度】
【出处】
无
【标注】
【答案】
$\left\{-\dfrac 12\right\}$
【解析】
首先题中不等式即$$-2-b\leqslant ax^2+|x-a|\leqslant 2-b,$$于是可以给跑龙套的 $b$ 发盒饭.条件可以转化为$$\forall x\in [-3,3],-2\leqslant ax^2+|x-a|\leqslant 1,$$即$$\forall x\in [-3,3],-ax^2-2\leqslant |x-a|\leqslant -ax^2+1,$$也即$$\forall x\in [-3,3],\begin{cases} ax^2-1\leqslant x-a \leqslant -ax^2+1,\\ \left(x-a\geqslant -ax^2-2\right)\lor \left(-x+a\geqslant -ax^2-2\right),\end{cases}$$也即$$\forall x\in [-3,3],\begin{cases} ax^2-x+a-1\leqslant 0,\\ ax^2+x-a-1\leqslant 0,\\ \left(ax^2+x-a+2\geqslant 0\right)\lor \left(ax^2-x+a+2\geqslant 0\right).\end{cases}$$接下来利用端点缩小 $a$ 的探索范围.取 $x=-3$,可以得到$$\begin{cases} 10a+2\leqslant 0,\\ 8a-4\leqslant 0,\\ \left(8a-1\geqslant 0\right)\lor\left(10a+5\geqslant 0\right),\end{cases}$$解得 $-\dfrac 12\leqslant a\leqslant -\dfrac 15$.
取 $x=3$,可以得到$$\begin{cases} 10a-4\leqslant 0,\\ 8a+2\leqslant 0,\\ (8a+5\geqslant 0)\lor (10a-1\geqslant 0),\end{cases}$$解得 $-\dfrac 58\leqslant a\leqslant -\dfrac 14$.
这样就得到了 $a$ 必然在区间 $\left[-\dfrac 12,-\dfrac 14\right]$ 上.这一轮进攻收获不小,接下来乘胜追击.
考虑对称轴处.注意到函数 $y=ax^2+|x-a|$,因此当 $x$ 与 $a$ 异号时,更容易在上界 $1$ 处出问题,因此取 $x=-\dfrac 1{2a}$(根据之前得到的 $a$ 的范围可知该对称轴一定在区间 $[-3,3]$ 内),可得$$\dfrac{1}{4a}-\dfrac{1}{2a}-a-1\leqslant 0,$$即$$4a^2+4a+1\leqslant0,$$因此 $a=-\dfrac 12$.
经过这两波猛烈的进攻以后,敌人已经举了白旗.例行公事,接受投降.
验证 $a=-\dfrac 12$ 时符合题意,这是显然的(事实上,此时函数 $y=ax^2+|x-a|$ 的图象如图).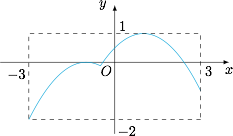
取 $x=3$,可以得到$$\begin{cases} 10a-4\leqslant 0,\\ 8a+2\leqslant 0,\\ (8a+5\geqslant 0)\lor (10a-1\geqslant 0),\end{cases}$$解得 $-\dfrac 58\leqslant a\leqslant -\dfrac 14$.
这样就得到了 $a$ 必然在区间 $\left[-\dfrac 12,-\dfrac 14\right]$ 上.这一轮进攻收获不小,接下来乘胜追击.
考虑对称轴处.注意到函数 $y=ax^2+|x-a|$,因此当 $x$ 与 $a$ 异号时,更容易在上界 $1$ 处出问题,因此取 $x=-\dfrac 1{2a}$(根据之前得到的 $a$ 的范围可知该对称轴一定在区间 $[-3,3]$ 内),可得$$\dfrac{1}{4a}-\dfrac{1}{2a}-a-1\leqslant 0,$$即$$4a^2+4a+1\leqslant0,$$因此 $a=-\dfrac 12$.
经过这两波猛烈的进攻以后,敌人已经举了白旗.例行公事,接受投降.
验证 $a=-\dfrac 12$ 时符合题意,这是显然的(事实上,此时函数 $y=ax^2+|x-a|$ 的图象如图).

答案
解析
备注