设函数 $f(x)=x^2-2ax+3-2a$ 的两个零点分别为 $x_1,x_2$，且在区间 $(x_1,x_2)$ 上恰好有两个正整数，求实数 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left(\dfrac 76,\dfrac 32\right]$
【解析】
考虑分离变量，方程$$x^2-2ax+3-2a=0$$即$$2a(x+1)=x^2+3.$$显然 $x=-1$ 不是方程的解，于是原方程等价于$$2a+2=x+1+\dfrac{4}{x+1},$$于是 $x_1,x_2$ 是函数 $g(x)=x+1+\dfrac{4}{x+1}$ 与直线 $y=2a+2$ 的公共点的横坐标．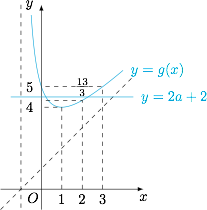
如图，可知区间 $(x_1,x_2)$ 上的两个正整数为 $1,2$，因此 $2a+2$ 的取值范围是 $\left(\dfrac{13}{3},5\right]$，进而可以解得 $a$ 的取值范围是 $\left(\dfrac 76,\dfrac 32\right]$．
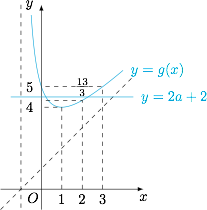如图，可知区间 $(x_1,x_2)$ 上的两个正整数为 $1,2$，因此 $2a+2$ 的取值范围是 $\left(\dfrac{13}{3},5\right]$，进而可以解得 $a$ 的取值范围是 $\left(\dfrac 76,\dfrac 32\right]$．
答案
解析
备注
