已知等腰三角形 $ABC$ 的底 $BC$ 长为 $6$，腰 $AB$ 长为 $5$．设 $D$ 是底边 $BC$ 上一点，以 $AD$ 为边向两边作等边三角形 $ADE,ADF$，设 $DE,DF$ 分别交 $AB,AC$ 于点 $M,N$，求证：当 $D$ 位于 $BC$ 中点时 $DM+DN$ 取得最小值．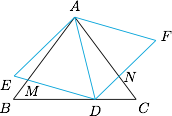
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
考虑到问题的对称性，我们采用对称的方式设参数：设 $\angle MDB=\dfrac {\pi}6-x$，$\angle NDC=\dfrac{\pi}6+x$，其中 $x\in [-\theta,\theta]$，$\theta$ 是临界状态时的角．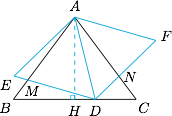
作 $AH\perp BC$ 于 $H$，则 $\angle DAH=x$，于是$$BD=3+4\tan x,CD=3-4\tan x,$$而$$\dfrac{DM}{\sin B}=\dfrac{BD}{\sin\left(B+\dfrac{\pi}6-x\right)},\dfrac{DN}{\sin C}=\dfrac{CD}{\sin\left(C+\dfrac{\pi}6+x\right)},$$于是\[\begin{split} \dfrac{DM+DN}{\sin B}&=\dfrac{3+4\tan x}{m\cos x-n\sin x}+\dfrac{3-4\tan x}{m\cos x+n\sin x}\\ &=\dfrac{6m\cos^2x+8n\sin^2x}{\cos x(m^2\cos^2x-n^2\sin^2x)},\end{split}\]其中 $m=\sin\left(B+\dfrac{\pi}6\right)$，$n=\cos\left(B+\dfrac{\pi}6\right)$．因此当 $x=0$ 时，$DM+DN$ 取得最小值，此时 $D$ 位于 $BC$ 的中点．
作 $AH\perp BC$ 于 $H$，则 $\angle DAH=x$，于是$$BD=3+4\tan x,CD=3-4\tan x,$$而$$\dfrac{DM}{\sin B}=\dfrac{BD}{\sin\left(B+\dfrac{\pi}6-x\right)},\dfrac{DN}{\sin C}=\dfrac{CD}{\sin\left(C+\dfrac{\pi}6+x\right)},$$于是\[\begin{split} \dfrac{DM+DN}{\sin B}&=\dfrac{3+4\tan x}{m\cos x-n\sin x}+\dfrac{3-4\tan x}{m\cos x+n\sin x}\\ &=\dfrac{6m\cos^2x+8n\sin^2x}{\cos x(m^2\cos^2x-n^2\sin^2x)},\end{split}\]其中 $m=\sin\left(B+\dfrac{\pi}6\right)$，$n=\cos\left(B+\dfrac{\pi}6\right)$．因此当 $x=0$ 时，$DM+DN$ 取得最小值，此时 $D$ 位于 $BC$ 的中点．
答案
解析
备注
