已知 $A,B$ 分别是椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的上顶点和下顶点,$F$ 为椭圆 $E$ 的右焦点.过 $F$ 作直线 $l$ 分别与椭圆交于 $C,D$,与 $y$ 轴交于点 $P$.直线 $AC$ 和 $BD$ 交于点 $Q$,求证:$\overrightarrow{OP}\cdot \overrightarrow{OQ}$ 为定值.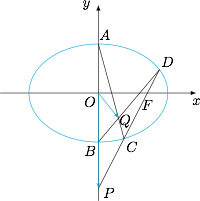

【难度】
【出处】
无
【标注】
【答案】
定值为 $b^2$
【解析】
设直线 $l$ 的方程为 $x=ty+c$,则点 $P$ 的坐标为 $\left(0,-\dfrac ct\right)$.设点 $Q$ 的坐标为 $(m,n)$,则$$\overrightarrow{OP}\cdot \overrightarrow{OQ}=-c\cdot\dfrac nt,$$于是只需要求出 $n$ 的值.
设 $D(x_1,y_1),C(x_2,y_2)$,根据题意,有$$\begin{cases} \dfrac{y_1+b}{x_1}=\dfrac{n+b}m,\\ \dfrac{y_2-b}{x_2}=\dfrac{n-b}{m},\end{cases}$$于是$$\dfrac{n+b}{n-b}=\dfrac{x_2(y_1+b)}{x_1(y_2-b)}.$$利用顶点弦代换,将椭圆方程改写为$$x^2=\dfrac{a^2}{b^2}(b+y)(b-y),$$从而有$$\left(\dfrac{n+b}{n-b}\right)^2=\dfrac{x_2^2(b+y_1)^2}{x_1^2(b-y_2)^2}=\dfrac{(b+y_1)(b+y_2)}{(b-y_1)(b-y_2)}=\dfrac{b^2+b(y_1+y_2)+y_1y_2}{b^2-b(y_1+y_2)+y_1y_2}.$$联立直线 $l$ 的方程与椭圆 $E$ 的方程,整理得$$\left(t^2+\dfrac{a^2}{b^2}\right)y^2+2tcy-b^2=0,$$从而$$\left(\dfrac{n+b}{n-b}\right)^2=\dfrac{b^2t^2+a^2-2tbc-b^2}{b^2t^2+a^2+2tbc-b^2}=\left(\dfrac{bt-c}{bt+c}\right)^2.$$又 $\dfrac{n+b}{n-b}$ 与 $x_1x_2$ 异号,也即与$$(ty_1+c)(ty_2+c)=t^2y_1y_2+tc(y_1+y_2)+c^2=\dfrac {a^2(c-bt)(c+bt)}{b^2t^2+a^2}$$异号,因此$$\dfrac{n+b}{n-b}=\dfrac{bt-c}{bt+c},$$解得 $n=-\dfrac{b^2t}c$,因此$$\overrightarrow{OP}\cdot \overrightarrow{OQ}=-c\cdot\dfrac nt=b^2,$$为定值.因此原命题得证.
设 $D(x_1,y_1),C(x_2,y_2)$,根据题意,有$$\begin{cases} \dfrac{y_1+b}{x_1}=\dfrac{n+b}m,\\ \dfrac{y_2-b}{x_2}=\dfrac{n-b}{m},\end{cases}$$于是$$\dfrac{n+b}{n-b}=\dfrac{x_2(y_1+b)}{x_1(y_2-b)}.$$利用顶点弦代换,将椭圆方程改写为$$x^2=\dfrac{a^2}{b^2}(b+y)(b-y),$$从而有$$\left(\dfrac{n+b}{n-b}\right)^2=\dfrac{x_2^2(b+y_1)^2}{x_1^2(b-y_2)^2}=\dfrac{(b+y_1)(b+y_2)}{(b-y_1)(b-y_2)}=\dfrac{b^2+b(y_1+y_2)+y_1y_2}{b^2-b(y_1+y_2)+y_1y_2}.$$联立直线 $l$ 的方程与椭圆 $E$ 的方程,整理得$$\left(t^2+\dfrac{a^2}{b^2}\right)y^2+2tcy-b^2=0,$$从而$$\left(\dfrac{n+b}{n-b}\right)^2=\dfrac{b^2t^2+a^2-2tbc-b^2}{b^2t^2+a^2+2tbc-b^2}=\left(\dfrac{bt-c}{bt+c}\right)^2.$$又 $\dfrac{n+b}{n-b}$ 与 $x_1x_2$ 异号,也即与$$(ty_1+c)(ty_2+c)=t^2y_1y_2+tc(y_1+y_2)+c^2=\dfrac {a^2(c-bt)(c+bt)}{b^2t^2+a^2}$$异号,因此$$\dfrac{n+b}{n-b}=\dfrac{bt-c}{bt+c},$$解得 $n=-\dfrac{b^2t}c$,因此$$\overrightarrow{OP}\cdot \overrightarrow{OQ}=-c\cdot\dfrac nt=b^2,$$为定值.因此原命题得证.
答案
解析
备注