已知 $n\geqslant 5$ 且 $n\in\mathbb N^*$，求证：$\dfrac{1}{n^2}+\dfrac{1}{(n+1)^2}+\cdots +\dfrac{1}{(2n)^2}>\dfrac{1}{2(n-1)}$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
考虑到不等式左边的代数结构，可以尝试利用积分放缩与裂项放缩．
如图．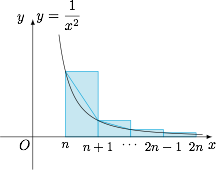
由于函数 $y=\dfrac{1}{x^2}$ 下凸，因此有矩形面积的和（注意最后一个矩形单独计算）大于曲边梯形的面积与小三角形面积之和，即\[\begin{split} \dfrac{1}{n^2}+\dfrac{1}{(n+1)^2}+\cdots +\dfrac{1}{(2n)^2}&>\int_{n}^{2n}\dfrac{1}{x^2}{\mathrm d}x+\dfrac{1}{(2n)^2}+\dfrac 12 \left[\dfrac 1{n^2}-\dfrac{1}{(2n)^2}\right]\\&=\left.\left(-\dfrac 1x\right)\right|_{n}^{2n}+\dfrac 12 \left[\dfrac 1{n^2}+\dfrac{1}{(2n)^2}\right]\\ &=\dfrac 1n-\dfrac{1}{2n}+\dfrac 12 \left[\dfrac 1{n^2}+\dfrac{1}{(2n)^2}\right] \\ &=\dfrac{4n+5}{8n^2},\end{split}\]接下来用分析法证明$$\dfrac{4n+5}{8n^2}\geqslant \dfrac{1}{2(n-1)},$$整理即为 $n\geqslant 5$，这显然成立．
综上所述，原不等式得证．
如图．
由于函数 $y=\dfrac{1}{x^2}$ 下凸，因此有矩形面积的和（注意最后一个矩形单独计算）大于曲边梯形的面积与小三角形面积之和，即\[\begin{split} \dfrac{1}{n^2}+\dfrac{1}{(n+1)^2}+\cdots +\dfrac{1}{(2n)^2}&>\int_{n}^{2n}\dfrac{1}{x^2}{\mathrm d}x+\dfrac{1}{(2n)^2}+\dfrac 12 \left[\dfrac 1{n^2}-\dfrac{1}{(2n)^2}\right]\\&=\left.\left(-\dfrac 1x\right)\right|_{n}^{2n}+\dfrac 12 \left[\dfrac 1{n^2}+\dfrac{1}{(2n)^2}\right]\\ &=\dfrac 1n-\dfrac{1}{2n}+\dfrac 12 \left[\dfrac 1{n^2}+\dfrac{1}{(2n)^2}\right] \\ &=\dfrac{4n+5}{8n^2},\end{split}\]接下来用分析法证明$$\dfrac{4n+5}{8n^2}\geqslant \dfrac{1}{2(n-1)},$$整理即为 $n\geqslant 5$，这显然成立．综上所述，原不等式得证．
答案
解析
备注
