如图，在正方形 $ABCD$ 内，有五个边长是不同的整数的正方形，且它们的一条对角线都在 $AC$ 上，且 $AB$ 长是 $2015$，求这五个正方形的面积之和的最大值及最小值．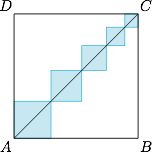
【难度】
【出处】
无
【标注】
【答案】
最小值为 $812055$，最大值为 $4020055$
【解析】
设这五个正方形的边长分别为 $x_i$（$i=1,2,3,4,5$），考虑函数 $f(x)=x^2$ 的割线，记 $l(m,n)$（$m\leqslant n$）为过函数 $y=f(x)$ 图象上的点 $M(m,m^2)$ 和 $N(n,n^2)$ 的割线（当 $m=n$ 时，将函数 $f(x)$ 在 $x=m$ 处的切线视为 $l(m,n)$）．显然当 $x<m$ 或 $x>n$ 时，$f(x)$ 的图象在 $l(m,n)$ 上方；当 $m<x<n$ 时，$f(x)$ 的图象在 $l(m,n)$ 下方，如图．
由于 $x_1,x_2,x_3,x_4,x_5$ 中至少有两个数在集合 $\{x\in\mathbb N^*\mid x\leqslant 401\lor x\geqslant 405\}$ 中，不妨设为 $x_1,x_2$；又 $x_1,x_2,x_3,x_4,x_5$ 中至少有四个数在集合 $\{x\in\mathbb N^*\mid x\leqslant 402\lor x\geqslant 404\}$ 中，设其中不同于 $x_1,x_2$ 的数为 $x_3,x_4$；剩下的一个数为 $x_5$，注意到 $l(401,405),l(402,404),l(403,403)$ 的斜率均相等，记为 $k$，则有$$\begin{cases} x_1^2\geqslant k(x_1-401)+401^2,\\ x_2^2\geqslant k(x_2-405)+405^2,\\ x_3^2\geqslant k(x_3-402)+402^2, \\ x_4^2\geqslant k(x_4-404)+404^2, \\ x_5^2\geqslant k(x_5-403)+403^2,\end{cases}$$累加有$$x_1^2+x_2^2+x_3^2+x_4^2+x_5^2\geqslant 401^2+402^2+403^2+404^2+405^2,$$等号当 $x_1=401,x_2=405,x_3=402,x_4=404,x_5=403$ 时取得，因此所求的最小值为 $812055$．
接下来考虑最大值，由于 $x_1,x_2,x_3,x_4,x_5$ 中至少有两个数在集合 $\{x\in\mathbb N^*\mid 4\leqslant x\leqslant 2005\}$ 中，不妨设为 $x_1,x_2$；又 $x_1,x_2,x_3,x_4,x_5$ 中至少有三个数在集合 $\{x\in\mathbb N^*\mid 3\leqslant x\leqslant 2006\}$ 中，设其中不同于 $x_1,x_2$ 的数为 $x_3$；又 $x_1,x_2,x_3,x_4,x_5$ 中至少有四个数在集合 $\{x\in\mathbb N^*\mid 2\leqslant x\leqslant 2007\}$ 中，设其中不同于 $x_1,x_2,x_3$ 的数为 $x_4$；剩下的一个数为 $x_5$，注意到 $l(4,2005),l(3,2006),l(2,2007),l(1,2008)$ 的斜率均相等，记为 $k'$，则有$$\begin{cases} x_1^2\leqslant k'(x_1-4)+4^2,\\ x_2^2\leqslant k'(x_2-2005)+2005^2,\\ x_3^2\leqslant k'(x_3-3)+3^2, \\ x_4^2\leqslant k'(x_4-2)+2^2, \\ x_5^2\leqslant k'(x_5-1)+1^2,\end{cases}$$累加有$$x_1^2+x_2^2+x_3^2+x_4^2+x_5^2\leqslant 1^2+2^2+3^2+4^2+2005^2,$$等号当 $x_1=4,x_2=2005,x_3=3,x_4=2,x_5=1$ 时取得，因此所求的最大值为 $4020055$．
由于 $x_1,x_2,x_3,x_4,x_5$ 中至少有两个数在集合 $\{x\in\mathbb N^*\mid x\leqslant 401\lor x\geqslant 405\}$ 中，不妨设为 $x_1,x_2$；又 $x_1,x_2,x_3,x_4,x_5$ 中至少有四个数在集合 $\{x\in\mathbb N^*\mid x\leqslant 402\lor x\geqslant 404\}$ 中，设其中不同于 $x_1,x_2$ 的数为 $x_3,x_4$；剩下的一个数为 $x_5$，注意到 $l(401,405),l(402,404),l(403,403)$ 的斜率均相等，记为 $k$，则有$$\begin{cases} x_1^2\geqslant k(x_1-401)+401^2,\\ x_2^2\geqslant k(x_2-405)+405^2,\\ x_3^2\geqslant k(x_3-402)+402^2, \\ x_4^2\geqslant k(x_4-404)+404^2, \\ x_5^2\geqslant k(x_5-403)+403^2,\end{cases}$$累加有$$x_1^2+x_2^2+x_3^2+x_4^2+x_5^2\geqslant 401^2+402^2+403^2+404^2+405^2,$$等号当 $x_1=401,x_2=405,x_3=402,x_4=404,x_5=403$ 时取得，因此所求的最小值为 $812055$．接下来考虑最大值，由于 $x_1,x_2,x_3,x_4,x_5$ 中至少有两个数在集合 $\{x\in\mathbb N^*\mid 4\leqslant x\leqslant 2005\}$ 中，不妨设为 $x_1,x_2$；又 $x_1,x_2,x_3,x_4,x_5$ 中至少有三个数在集合 $\{x\in\mathbb N^*\mid 3\leqslant x\leqslant 2006\}$ 中，设其中不同于 $x_1,x_2$ 的数为 $x_3$；又 $x_1,x_2,x_3,x_4,x_5$ 中至少有四个数在集合 $\{x\in\mathbb N^*\mid 2\leqslant x\leqslant 2007\}$ 中，设其中不同于 $x_1,x_2,x_3$ 的数为 $x_4$；剩下的一个数为 $x_5$，注意到 $l(4,2005),l(3,2006),l(2,2007),l(1,2008)$ 的斜率均相等，记为 $k'$，则有$$\begin{cases} x_1^2\leqslant k'(x_1-4)+4^2,\\ x_2^2\leqslant k'(x_2-2005)+2005^2,\\ x_3^2\leqslant k'(x_3-3)+3^2, \\ x_4^2\leqslant k'(x_4-2)+2^2, \\ x_5^2\leqslant k'(x_5-1)+1^2,\end{cases}$$累加有$$x_1^2+x_2^2+x_3^2+x_4^2+x_5^2\leqslant 1^2+2^2+3^2+4^2+2005^2,$$等号当 $x_1=4,x_2=2005,x_3=3,x_4=2,x_5=1$ 时取得，因此所求的最大值为 $4020055$．
答案
解析
备注
