已知椭圆 $C:\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$,斜率为 $1$ 的直线 $l$ 与椭圆交于 $A,B$ 两点,点 $M(4,0)$,直线 $AM$ 与椭圆 $C$ 交于点 $A_1$,直线 $BM$ 与椭圆交于点 $B_1$,求证:直线 $A_1B_1$ 恒过定点.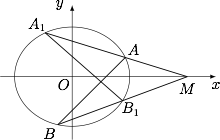

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设 $A(2\cos 2\alpha,\sqrt 3\sin 2\alpha)$,$B(2\cos 2\beta,\sqrt 3\sin 2\beta)$,$A_1(2\cos 2\alpha_1,\sqrt 3\sin 2\alpha_1)$,$B_1(2\cos 2\beta_1,\sqrt 3\sin 2\beta_1)$,于是直线 $AB$ 的斜率为 $1$ 等价于$$-\dfrac{\sqrt 3}2\cdot \dfrac{1}{\tan(\alpha+\beta)}=1, \text{即} \tan(\alpha+\beta)=-\dfrac{\sqrt 3}2.$$而直线 $AA_1$ 和直线 $BB_1$ 均过点 $M(4,0)$,因此$$\tan\alpha\cdot\tan\alpha_1=\tan\beta\cdot \tan\beta_1=\dfrac 13.$$这样就有$$\tan(\alpha+\beta)=\dfrac{\dfrac{1}{3\tan\alpha_1}+\dfrac{1}{3\tan\beta_1}}{1-\dfrac{1}{3\tan\alpha_1}\cdot\dfrac{1}{3\tan\beta_1}}=-\dfrac{\sqrt 3}2,$$整理得$$6(\tan\alpha_1+\tan\beta_1)=-9\sqrt 3\tan\alpha_1\cdot \tan\beta_1+\sqrt 3.$$考虑到直线 $A_1B_1$ 的方程为$$(1-\tan\alpha_1\cdot\tan\beta_1)\cdot \dfrac x2+(\tan\alpha_1+\tan\beta_1)\cdot \dfrac y{\sqrt 3}=1+\tan\alpha_1\cdot\tan\beta_1,$$即$$\dfrac{y}{\sqrt 3}(\tan\alpha_1+\tan\beta_1)=\left(1+\dfrac{x}2\right)\tan\alpha_1\cdot \tan\beta_1+1-\dfrac x2,$$由$$\dfrac{y}{\sqrt 3}:6=\left(1+\dfrac x2\right):-9\sqrt 3=\left(1-\dfrac x2\right):\sqrt 3,$$解得$$x=\dfrac 52,y=-\dfrac 32,$$因此直线 $A_1B_1$ 恒过点 $\left(\dfrac 52,-\dfrac 32\right)$.
答案
解析
备注