过点 $T(2,3)$ 作直线 $l$ 交椭圆 $\dfrac{x^2}4+y^2=1$ 于两个不同的点 $P,Q$，过 $P,Q$ 作椭圆的切线，两条切线交于点 $M$，$O$ 为原点，已知四边形 $POQM$ 的面积为 $4$，求直线 $l$ 的方程．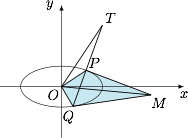
【难度】
【出处】
无
【标注】
【答案】
$y=x+1$ 或 $y=\dfrac{11}{4}x-\dfrac 52$
【解析】
考虑仿射变换 $x=x'$，$y=\dfrac 12y'$，则椭圆变为 $x'^2+y'^2=4$，点 $T(2,3)$ 变为 $T'(2,6)$．设 $P,Q,M$ 的对应点分别为 $P',Q',M'$，则四边形 $P'OQ'M'$ 的面积为 $8$．
设 $O$ 到直线 $P'Q'$ 的距离为 $d$，由射影定理 $d\cdot |OM'|=|OP'|^2$，于是 $|OM'|=\dfrac 4d$，从而四边形 $P'OQ'M'$ 的面积$$S=\dfrac 12\cdot |P'Q'|\cdot |OM'|=\sqrt{4-d^2}\cdot \dfrac 4d=8,$$解得 $d^2=\dfrac 45$．设直线 $P'Q':y'=k'(x-2)+6$，则有$$\dfrac{(2k'-6)^2}{1+k'^2}=\dfrac 45,$$解得 $k'=2$ 或 $k'=\dfrac{11}{2}$，于是直线 $l$ 的方程为 $y=x+1$ 或 $y=\dfrac{11}{4}x-\dfrac 52$．
设 $O$ 到直线 $P'Q'$ 的距离为 $d$，由射影定理 $d\cdot |OM'|=|OP'|^2$，于是 $|OM'|=\dfrac 4d$，从而四边形 $P'OQ'M'$ 的面积$$S=\dfrac 12\cdot |P'Q'|\cdot |OM'|=\sqrt{4-d^2}\cdot \dfrac 4d=8,$$解得 $d^2=\dfrac 45$．设直线 $P'Q':y'=k'(x-2)+6$，则有$$\dfrac{(2k'-6)^2}{1+k'^2}=\dfrac 45,$$解得 $k'=2$ 或 $k'=\dfrac{11}{2}$，于是直线 $l$ 的方程为 $y=x+1$ 或 $y=\dfrac{11}{4}x-\dfrac 52$．
答案
解析
备注
