设椭圆的方程为 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$（$a>b>0$），线段 $PQ$ 是过左焦点 $F$ 且不与 $x$ 轴垂直的焦点弦．若在左准线上存在点 $R$，使 $\triangle PQR$ 为正三角形，求椭圆的离心率 $e$ 的取值范围，并用 $e$ 表示直线 $PQ$ 的斜率．
【难度】
【出处】
无
【标注】
【答案】
$\left(\dfrac{\sqrt 3}3,1\right)$，$k_{PQ}=\pm\dfrac{1}{\sqrt{3e^2-1}}$
【解析】
如图，设弦 $PQ$ 的中点为 $M$，$P,Q,M$ 在左准线上的投影分别为 $P_1,Q_1,M_1$．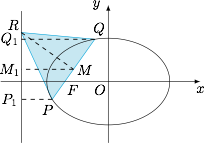
设 $|PP_1|=m$，$|QQ_1|=n$，则 $|PF|=em$，$|QF|=en$，根据题意，有$$|RM|=\dfrac{\sqrt 3}2|PQ|=\dfrac{\sqrt 3}2(m+n)e,$$于是由 $|RM|>|M_1M|$（因为 $PQ$ 不垂直于 $x$ 轴）可得$$\dfrac{\sqrt 3}2(m+n)e>\dfrac 12(m+n),$$从而可得椭圆的离心率的取值范围是 $\left(\dfrac{\sqrt 3}3,1\right)$．
设直线 $PQ$ 的倾斜角大小为 $\theta$，则$$\sin\theta=\cos\angle RMM_1=\dfrac{|M_1M|}{|RM|}=\dfrac{1}{e\sqrt 3},$$于是直线 $PQ$ 的斜率为$$\tan\theta=\pm\dfrac{1}{\sqrt{3e^2-1}}.$$
设 $|PP_1|=m$，$|QQ_1|=n$，则 $|PF|=em$，$|QF|=en$，根据题意，有$$|RM|=\dfrac{\sqrt 3}2|PQ|=\dfrac{\sqrt 3}2(m+n)e,$$于是由 $|RM|>|M_1M|$（因为 $PQ$ 不垂直于 $x$ 轴）可得$$\dfrac{\sqrt 3}2(m+n)e>\dfrac 12(m+n),$$从而可得椭圆的离心率的取值范围是 $\left(\dfrac{\sqrt 3}3,1\right)$．设直线 $PQ$ 的倾斜角大小为 $\theta$，则$$\sin\theta=\cos\angle RMM_1=\dfrac{|M_1M|}{|RM|}=\dfrac{1}{e\sqrt 3},$$于是直线 $PQ$ 的斜率为$$\tan\theta=\pm\dfrac{1}{\sqrt{3e^2-1}}.$$
答案
解析
备注
