如图，在 $\triangle ABC$ 中，$AB=AC$，$I$ 为 $\triangle ABC$ 的内心．以 $A$ 为圆心，$AB$ 为半径作圆 $\varGamma_1$，以 $I$ 为圆心，$IB$ 为半径作圆 $\varGamma_2$，过点 $B,I$ 的圆 $\varGamma_3$ 与 $\varGamma_1,\varGamma_2$ 分别交于点 $P,Q$（不同于点 $B$）．设 $IP$ 与 $BQ$ 交于点 $R$．证明：$BR\perp CR$．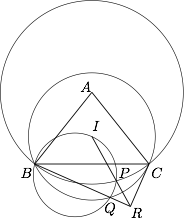
【难度】
【出处】
2017年全国高中数学联赛A卷（二试）
【标注】
【答案】
略
【解析】
如图，连接 $IB,IC,IQ,PB,PC$．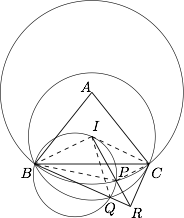
由于点 $Q$ 在圆 $\Gamma_2$ 上，故 $IB=IQ$，所以\[\angle IBQ=\angle IQB.\]又 $B,I,P,Q$ 四点共圆，所以 $\angle IQB=\angle IPB$，于是 $\angle IBQ=\angle IPB$，故 $\triangle IBP$ 与 $\triangle IRB$ 相似，从而有 $\angle IRB=\angle IBP$，且\[\dfrac{IB}{IR}=\dfrac{IP}{IB},\]注意到 $AB=AC$，且 $I$ 为 $\triangle ABC$ 的内心，故 $IB=IC$，所以\[\dfrac{IC}{IR}=\dfrac{IP}{IC},\]于是 $\triangle ICP$ 与 $\triangle IRC$ 相似，故\[\angle IRC=\angle ICP.\]又点 $P$ 在圆 $\Gamma_1$ 的弧 $BC$ 上，故\[\angle BPC=180^\circ-\dfrac 12\angle A,\]因此\[\begin{split}\angle BRC&=\angle IRB+\angle IRC\\
&=\angle IBP+\angle ICP\\
&=360^\circ-\left(90^\circ+\dfrac 12\angle A\right)-\left(180^\circ-\dfrac 12\angle A\right)\\
&=90^\circ,\end{split}\]故 $BR\perp CR$．
由于点 $Q$ 在圆 $\Gamma_2$ 上，故 $IB=IQ$，所以\[\angle IBQ=\angle IQB.\]又 $B,I,P,Q$ 四点共圆，所以 $\angle IQB=\angle IPB$，于是 $\angle IBQ=\angle IPB$，故 $\triangle IBP$ 与 $\triangle IRB$ 相似，从而有 $\angle IRB=\angle IBP$，且\[\dfrac{IB}{IR}=\dfrac{IP}{IB},\]注意到 $AB=AC$，且 $I$ 为 $\triangle ABC$ 的内心，故 $IB=IC$，所以\[\dfrac{IC}{IR}=\dfrac{IP}{IC},\]于是 $\triangle ICP$ 与 $\triangle IRC$ 相似，故\[\angle IRC=\angle ICP.\]又点 $P$ 在圆 $\Gamma_1$ 的弧 $BC$ 上，故\[\angle BPC=180^\circ-\dfrac 12\angle A,\]因此\[\begin{split}\angle BRC&=\angle IRB+\angle IRC\\&=\angle IBP+\angle ICP\\
&=360^\circ-\left(90^\circ+\dfrac 12\angle A\right)-\left(180^\circ-\dfrac 12\angle A\right)\\
&=90^\circ,\end{split}\]故 $BR\perp CR$．
答案
解析
备注
