已知适合不等式 $\left|x^2-4x+a\right|+|x-3|\leqslant 5$ 的 $x$ 的最大值为 $3$，求实数 $a$ 的值，并解该不等式．
【难度】
【出处】
无
【标注】
【答案】
$a=8$，不等式的解集为 $[2,3]$
【解析】
设 $f(x)=\left|x^2-4x+a\right|$，$g(x)=5-|x-3|$，则$$f(3)=\left|a-3\right|\leqslant g(3)=5,$$于是 $|a-3|\leqslant 5$．
情形一 $|a-3|=5$．此时 $a=8$ 或 $a=-2$，如图．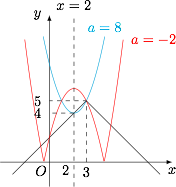
不难得到 $a=8$ 符合题意，此时不等式的解集为 $[2,3]$．
情形二 $|a-3|<5$．此时 $-2<a<8$．
由于 $f(3)<g(3)$，而 $f(9)\geqslant 0>g(9)$，于是函数 $y=f(x)-g(x)$ 在区间 $(3,9)$ 上必有零点 $x_0$，与满足不等式的 $x$ 的最大值为 $3$ 矛盾．
综上，实数 $a$ 的值为 $8$，该不等式的解集为 $[2,3]$．
不难得到 $a=8$ 符合题意，此时不等式的解集为 $[2,3]$．由于 $f(3)<g(3)$，而 $f(9)\geqslant 0>g(9)$，于是函数 $y=f(x)-g(x)$ 在区间 $(3,9)$ 上必有零点 $x_0$，与满足不等式的 $x$ 的最大值为 $3$ 矛盾．
综上，实数 $a$ 的值为 $8$，该不等式的解集为 $[2,3]$．
答案
解析
备注
