已知点 $A(0,3)$，$B(1,0)$，$C(3,m)$，以 $C$ 为圆心作半径为 $\dfrac{\sqrt {10}}3$ 的圆 $C$．
【难度】
【出处】
无
【标注】
-
若对线段 $AB$ 上的任意一点 $P$，均存在过 $P$ 的直线与圆 $C$ 相交于点 $M,N$（$|PM|<|PN|$），且 $|PM|=|MN|$，求 $m$ 的取值范围；标注答案$\left[2,\sqrt 6\right]$解析“过 $P$ 的某条直线与圆 $C$ 相交于点 $M,N$（$|PM|<|PN|$），且 $|PM|=|MN|$”的充要条件是“$\dfrac{PC-r}{PC+r}\leqslant \dfrac 12$（$r$ 是圆 $C$ 的半径）”．即 $|PC|\leqslant 3r$．
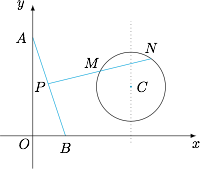题意即 $C$ 到线段 $AB$ 上任意一点 $P$ 的距离不大于 $3r$，这当且仅当$$|CA|\leqslant 3r\land |CB|\leqslant 3r.$$解得 $2\leqslant m\leqslant \sqrt 6$． -
若线段 $AB$ 上存在一点 $P$，使过 $P$ 的某条直线与圆 $C$ 相交于点 $M,N$（$|PM|<|PN|$），且 $|PM|=|MN|$，求 $m$ 的取值范围．标注答案$\left[-\sqrt 6,4\right]$解析题意在线段 $AB$ 上存在一点 $P$，到点 $C$ 的距离不大于 $3r$，先探索充分条件：若 $|CA|\leqslant 3r$ 或 $|CB|\leqslant 3r$，此时的 $m$ 一定满足条件，解得$$-\sqrt 6\leqslant m\leqslant 4.$$若 $m<-\sqrt 6$，此时 $C$ 到线段 $AB$ 上的点的距离的最小值为 $|CB|$，显然不满足；若 $m>4$，此时 $C$ 到线段 $AB$ 上的点的距离的最小值为 $|CA|$，也不满足，综上知 $m\in[-\sqrt 6,4]$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
