已知一个正三棱柱的底面边长为 $1$，且两个侧面的异面对角线互相垂直，则它的侧棱长为 \((\qquad)\)
【难度】
【出处】
2008年全国高中数学联赛福建省预赛
【标注】
【答案】
B
【解析】
如图．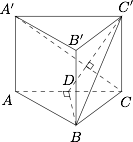
由于 $B$ 在平面 $AC'$ 上的投影为 $AC$ 的中点 $D$，于是$$BC' \perp A'C \Rightarrow A'C \perp CD \Rightarrow\dfrac{{AA'}}{{AC}} = \dfrac{{CD}}{{CC'}},$$所以 $A{A'^2} = \dfrac{1}{2}$，$AA' = \dfrac{{\sqrt 2 }}{2}$．
由于 $B$ 在平面 $AC'$ 上的投影为 $AC$ 的中点 $D$，于是$$BC' \perp A'C \Rightarrow A'C \perp CD \Rightarrow\dfrac{{AA'}}{{AC}} = \dfrac{{CD}}{{CC'}},$$所以 $A{A'^2} = \dfrac{1}{2}$，$AA' = \dfrac{{\sqrt 2 }}{2}$．
题目
答案
解析
备注
