如图,${F_1}$,$ {F_2}$ 分别是椭圆 $C:\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1\left( {a > b > 0} \right)$ 的左、右焦点,$A$ 是椭圆 $C$ 的顶点,$B$ 是直线 $A{F_2}$ 与椭圆 $C$ 的另一个交点,$\angle {F_1}A{F_2} = {60^\circ}$.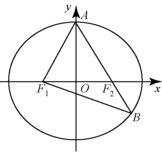

【难度】
【出处】
2012年高考安徽卷(文)
【标注】
-
求椭圆 $C$ 的离心率;标注答案$\dfrac12$解析由 $\angle F_1AF_2=60^\circ$,可得 $a=2c$,所以离心率为 $\dfrac12$.
-
已知 $\triangle A{F_1}B$ 面积为 $40\sqrt 3 $,求 $a $,$ b$ 的值.标注答案$ a = 10$,$b = 5\sqrt 3$解析设 $\left| {B{F_2}} \right| = m$,则 $\left| {B{F_1}} \right| = 2a - m$.
在 $\triangle B{F_1}{F_2}$ 中,由余弦定理得\[{\left| {B{F_1}} \right|^2} = {\left| {B{F_2}} \right|^2} + {\left| {{F_1}{F_2}} \right|^2} - 2\left| {B{F_2}} \right| \times \left| {{F_1}{F_2}} \right| \times \cos {120^\circ},\]整理得\[ {\left(2a - m\right)^2} = {m^2} + {a^2} + am,\]解得 $m = \dfrac{3}{5}a$.
又 $\triangle A{F_1}B$ 面积 $S = \dfrac{1}{2} \times \left| {{A}{F_1}} \right| \times \left| {AB} \right| \times \sin {60^\circ}$,整理得\[\dfrac{1}{2} \times a \times \left({a + \dfrac{3}{5}a} \right)\times \dfrac{\sqrt 3 }{2} = 40\sqrt 3,\]解得 $ a = 10$,$c = 5$,$b = 5\sqrt 3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2