如图1,在 ${\mathrm{Rt}} \triangle ABC$ 中,$\angle C = 90^\circ , BC = 3 , AC = 6$.$D , E$ 分别是 $AC , AB$ 上的点,且 $DE\parallel BC$,$DE = 2$,将 $\triangle ADE$ 沿 $DE$ 折起到 $\triangle {A_1}DE$ 的位置,使 ${A_1}C \perp CD$,如图2.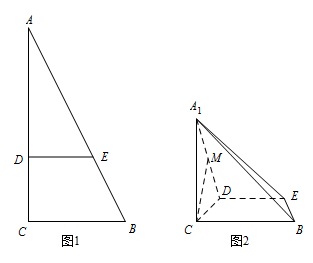

【难度】
【出处】
2012年高考北京卷(理)
【标注】
-
求证:${A_1}C \perp $ 平面 $BCDE$;标注答案略解析$\because $ $CD \perp DE$,${A_1}D \perp DE$,$\therefore $ $DE \perp $ 平面 ${A_1}CD$,
又 $\because $ ${A_1}C \subset $ 平面 ${A_1}CD$,$\therefore$ $ {A_1}C \perp DE$,
又 ${A_1}C \perp CD$,$\therefore $ ${A_1}C \perp $ 平面 $BCDE$. -
若 $M$ 是 ${A_1}D$ 的中点,求 $CM$ 与平面 ${A_1}BE$ 所成角的大小;标注答案略解析如图建系 $C - xyz$,
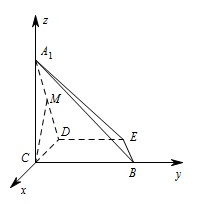 则\[D\left( { - 2,0,0} \right), A_1\left( {0,0,2\sqrt 3 } \right) , B\left( {0,3,0} \right) , E\left( { - 2,2,0} \right),\]所以\[\begin{split}\overrightarrow {{A_1}B} & = \left( {0,3, - 2\sqrt 3 } \right) , \\ \overrightarrow {BE} & = \left( { - 2, - 1,0} \right).\end{split}\]设平面 ${A_1}BE$ 的法向量为 $\overrightarrow n = \left( {x,y,z} \right)$,则\[\begin{cases}\overrightarrow {{A_1}B} \cdot \overrightarrow n = 0, \\
则\[D\left( { - 2,0,0} \right), A_1\left( {0,0,2\sqrt 3 } \right) , B\left( {0,3,0} \right) , E\left( { - 2,2,0} \right),\]所以\[\begin{split}\overrightarrow {{A_1}B} & = \left( {0,3, - 2\sqrt 3 } \right) , \\ \overrightarrow {BE} & = \left( { - 2, - 1,0} \right).\end{split}\]设平面 ${A_1}BE$ 的法向量为 $\overrightarrow n = \left( {x,y,z} \right)$,则\[\begin{cases}\overrightarrow {{A_1}B} \cdot \overrightarrow n = 0, \\
\overrightarrow {BE} \cdot \overrightarrow n = 0 ,\\
\end{cases}\]即\[\begin{cases}3y - 2\sqrt 3 z = 0, \\
- 2x - y = 0, \\
\end{cases}\]解得\[\begin{cases}z = \dfrac{\sqrt 3 }{2}y, \\
x = - \dfrac{y}{2} ,\\
\end{cases}\]因此可取 $\overrightarrow n = \left( { - 1,2,\sqrt 3 } \right)$.
又 $M\left( { - 1,0,\sqrt 3 } \right)$,可知 $\overrightarrow {CM} = \left( { - 1,0,\sqrt 3 } \right)$,故\[\begin{split}\cos \left \langle \overrightarrow {CM},\overrightarrow n \right \rangle = \dfrac{{\overrightarrow {CM} \cdot \overrightarrow n }}{{ \left|\overrightarrow {CM} \right| \cdot \left|\overrightarrow n \right|}} = \dfrac{1 + 3}{{\sqrt {1 + 4 + 3} \cdot \sqrt {1 + 3} }} = \dfrac{\sqrt 2 }{2},\end{split}\]所以 $CM$ 与平面 ${A_1}BE$ 所成角的大小为 $45^\circ $. -
线段 $BC$ 上是否存在点 $P$,使平面 ${A_1}DP$ 与平面 ${A_1}BE$ 垂直?说明理由.标注答案略解析设线段 $BC$ 上存在点 $P$,设 $P$ 点坐标为 $\left( {0,a,0} \right)$,则 $a \in \left[ {0,3} \right]$,则\[\begin{split}\overrightarrow {{A_1}P} & = \left( {0,a, - 2\sqrt 3 } \right) , \\ \overrightarrow {DP} & = \left( {2,a,0} \right).\end{split}\]设平面 ${A_1}DP$ 的法向量为 $\overrightarrow {n_1} = \left( {{x_1},{y_1},{z_1}} \right)$,则\[\begin{cases}a{y_1} - 2\sqrt 3 {z_1} = 0, \\
2{x_1} + a{y_1} = 0 ,\\
\end{cases}\]解得\[\begin{cases}{z_1} = \dfrac{\sqrt 3 }{6}a{y_1}, \\
{x_1} = - \dfrac{1}{2}a{y_1}, \\
\end{cases}\]所以可取 $\overrightarrow {n_1} = \left( { - 3a,6,\sqrt 3 a} \right)$.
假设平面 ${A_1}DP$ 与平面 ${A_1}BE$ 垂直,则 $\overrightarrow {n_1} \cdot \overrightarrow n = 0$,因此\[3a + 12 + 3a = 0,\]解得\[a=-2,\]又 $0 \leqslant a \leqslant 3$,可知在线段 $BC$ 上不存在点 $P$,使平面 ${A_1}DP$ 与平面 ${A_1}BE$ 垂直.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3