如图 $ 1 $，在 ${ \mathrm {Rt} }\triangle ABC$ 中，$\angle C = 90^\circ $，$D$，$E$ 分别是 $AC$，$AB$ 的中点，点 $F$ 为线段 $CD$ 上的一点，将 $\triangle ADE$ 沿 $DE$ 折起到 $\triangle {A_1}DE$ 的位置，使 ${A_1}F \perp CD$，如图 $ 2 $．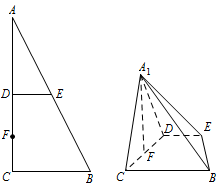
【难度】
【出处】
2012年高考北京卷（文）
【标注】
-
求证：$DE\parallel $ 平面 ${A_1}CB$；标注答案略解析因为 $ D$，$E $ 分别为 $ AC$，$AB $ 的中点，所以 $ DE\parallel BC $．
又因为 $ DE\not\subset $ 平面 $ A_1CB $，$ BC\subset $ 平面 $ A_1CB $，所以 $ DE\parallel $ 平面 $ A_1CB $． -
求证：${A_1}F \perp BE$；标注答案略解析由已知得 $ AC\perp BC $ 且 $ DE\parallel BC $，
所以 $ DE\perp AC $．
所以 $ DE\perp A_1D$，$DE\perp CD $．
所以 $ DE\perp $ 平面 $ A_1DC $．
而 $ A_1F \subset$ 平面 $ A_1DC $，
所以 $ DE\perp A_1F $．
又因为 $ A_1F\perp CD $，
所以 $ A_1F\perp $ 平面 $ BCDE $．
所以 $ A_1F\perp BE $． -
线段 ${A_1}B$ 上是否存在点 $Q$，使 ${A_1}C \perp $ 平面 $DEQ$？说明理由．标注答案线段 $ A_1B $ 上存在点 $ Q $，使 $ A_1C\perp $ 平面 $ DEQ $．理由略解析线段 $ A_1B $ 上存在点 $ Q $，使 $ A_1C\perp $ 平面 $ DEQ $．
理由如下：
如图，分别取 $ A_1C$，$A_1B $ 的中点 $ P$，$Q $，则 $ PQ\parallel BC $．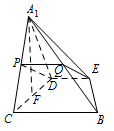
又因为 $ DE\parallel BC $，
所以 $ DE\parallel PQ $．
所以平面 $ DEQ $ 即为平面 $ DEP $．
由（2）知，$ DE\perp $ 平面 $ A_1DC $，
所以 $ DE\perp A_1C $．
又因为 $ P $ 是等腰三角形 $ DA_1C $ 底边 $ A_1C $ 的中点，
所以 $ A_1C\perp DP $．
所以 $ A_1C\perp $ 平面 $ DEP $．
从而 $ A_1C\perp $ 平面 $ DEQ $．
故线段 $ A_1B $ 上存在点 $ Q $，使得 $ A_1C\perp $ 平面 $ DEQ $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
