如图，已知 $A,B$ 两点在椭圆 $C:\dfrac{{{x^2}}}{m} + {y^2} = 1$（$m > 1$），直线 $AB$ 上两个不同的点 $P,Q$ 满足 $\left| {AP} \right|:\left| {PB} \right| = \left| {AQ} \right|:\left| {QB} \right|$，且 $P$ 点的坐标为 $\left( {1, 0} \right)$．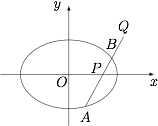
【难度】
【出处】
2008年武汉大学自主招生保送生测试
【标注】
-
若 $m = 2$，求证：点 $Q$ 在椭圆准线上；标注答案略解析若 $m = 2$，则 $P$ 点为右焦点．过 $Q$ 作 $x$ 轴的垂线 $l$，过 $A$、$B$ 作 $l$ 的垂线，垂足分别为 $M$、$N$，如图，
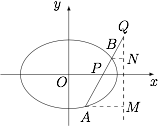则$$\dfrac{{AQ}}{{QB}} = \dfrac{{AM}}{{BN}} = \dfrac{{AP}}{{PB}}.$$由同一法容易证明 $l$ 为准线． -
若 $m$ 为大于 $1$ 的常数，求点 $Q$ 的轨迹方程．标注答案$x = m$解析设直线 $l$ 为 $\begin{cases} x = 1 + t,\\y = kt,\end{cases}$ 其中 $A,B,Q$ 对应的参数分别为 ${t_1},{t_2},{t_0}$，则$$\left| {\dfrac{{{t_1}}}{{{t_2}}}} \right| = \left| {\dfrac{{{t_0} - {t_1}}}{{{t_0} - {t_2}}}} \right|,$$易知 $\dfrac{{{t_1}}}{{{t_2}}} \ne \dfrac{{{t_0} - {t_1}}}{{{t_0} - {t_2}}}$，所以 $\dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{{t_0} - {t_1}}}{{{t_2} - {t_0}}}$，即$${t_0} = \dfrac{{2{t_1}{t_2}}}{{{t_1} + {t_2}}},$$联立直线与椭圆，有$$\dfrac{1}{m}{\left( {t + 1} \right)^2} + {k^2}{t^2} - 1 = 0,$$即$$\left( {{k^2} + \dfrac{1}{m}} \right){t^2} + \dfrac{2}{m}t + \dfrac{1}{m} - 1 = 0,$$所以$${t_0} = \dfrac{{2\left( {\frac{1}{m} - 1} \right)}}{{ - \frac{2}{m}}} = m - 1,$$于是点 $Q$ 的轨迹方程为 $x = m$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
