从 $O$ 点发出两条射线 ${l_1},{l_2}$，已知直线 $l$ 分别交 ${l_1},{l_2}$ 于 $A,B$ 两点，且 ${S_{\triangle OAB}} = c$（$c$ 为定值），记 $AB$ 中点为 $D$，$D$ 随着 $A,B$ 的运动构成轨迹 $\Gamma$．求证：
【难度】
【出处】
2012年北京大学保送生试题
【标注】
-
$D$ 的轨迹 $\Gamma$ 关于 $\angle AOB$ 的角平分线反射对称；标注答案略解析根据条件的对称性即得．
-
轨迹 $\Gamma$ 为双曲线．标注答案略解析以 ${l_1},{l_2}$ 的角平分线所在直线为 $x$ 轴建立如图所示的直角坐标系．
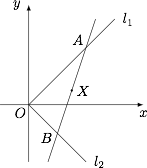设 $\angle AOx = \angle BOx = \alpha $，$OA = a,OB = b$，$X\left( {x,y} \right)$，
则$${S_{\Delta OAB}} = \dfrac{1}{2}ab\sin 2\alpha = c,$$所以 $ab = \dfrac{{2c}}{{\sin 2\alpha }}$．
因为 $ A\left( {a\cos \alpha ,a\sin \alpha } \right),B\left( {b\cos \alpha , - b\sin \alpha } \right)$，所以$$\begin{cases}x = \dfrac{{a\cos \alpha + b\cos \alpha }}{2}, \\ y = \dfrac{{a\sin \alpha - b\sin \alpha }}{2}, \end{cases}$$所以$$\begin{cases}\dfrac{x}{{\cos \alpha }} = \dfrac{{a + b}}{2}, \\ \dfrac{y}{{\sin \alpha }} = \dfrac{{a - b}}{2}.\end{cases}$$两式平方相减得 $\dfrac{{{x^2}}}{{{{\cos }^2}\alpha }} - \dfrac{{{y^2}}}{{{{\sin }^2}\alpha }} = ab = \dfrac{{2c}}{{\sin 2\alpha }}$，
所以，$X$ 的轨迹为双曲线（的一支），且关于 $\angle AOB$ 的角平分线反射对称．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
