如图,四面体 $ABCD$ 中,$AB$ 和 $CD$ 为对棱.设 $AB = a$,$CD = b$,且异面直线 $AB$ 与 $CD$ 的距离为 $d$,夹角为 $\theta $.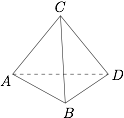

【难度】
【出处】
2010年同济大学自主招生保送生测试
【标注】
-
若 $\theta = \dfrac{{{\pi }}}{2}$,且棱 $AB$ 垂直于平面 $BCD$,求四面体 $ABCD$ 的体积;标注答案$\dfrac{1}{6}abd$解析如图,
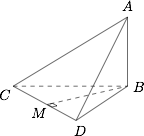 在平面 $BCD$ 中,作 $BM \perp CD$ 于 $M$,则 $BM = d$.所以$$\begin{split}{V_{A - BCD}}&= \dfrac{1}{3} \cdot AB \cdot {S_{\triangle BCD}}\\ &= \dfrac{1}{3} \cdot a \cdot \dfrac{1}{2}b \cdot d\\ &= \dfrac{1}{6}abd.\end{split}$$
在平面 $BCD$ 中,作 $BM \perp CD$ 于 $M$,则 $BM = d$.所以$$\begin{split}{V_{A - BCD}}&= \dfrac{1}{3} \cdot AB \cdot {S_{\triangle BCD}}\\ &= \dfrac{1}{3} \cdot a \cdot \dfrac{1}{2}b \cdot d\\ &= \dfrac{1}{6}abd.\end{split}$$ -
当 $\theta = \dfrac{{{\pi }}}{2}$ 时,证明:四面体 $ABCD$ 的体积为一定值;标注答案略解析如图,过 $A$ 作 $AM\perp CD$ 于 $M$,连结 $BM$.
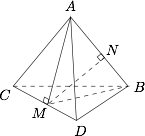 由 $CD\perp$ 平面 $ABM$,可得平面 $AMB \perp$ 平面 $BCD$,过 $M$ 作 $MN \perp AB$ 于 $N$,则 $MN = d$,因此有$${V_{A - BCD}} = \dfrac{1}{3}{S_{\triangle AMB}} \cdot CD = \dfrac{1}{6}abd.$$
由 $CD\perp$ 平面 $ABM$,可得平面 $AMB \perp$ 平面 $BCD$,过 $M$ 作 $MN \perp AB$ 于 $N$,则 $MN = d$,因此有$${V_{A - BCD}} = \dfrac{1}{3}{S_{\triangle AMB}} \cdot CD = \dfrac{1}{6}abd.$$ -
求四面体 $ABCD$ 的体积.标注答案$\dfrac{1}{6}abd\sin \theta $解析如图,将四面体补成平行六面体 $ABGH - ECFD$,则 $AB$ 与 $CD$ 的距离即平行六面体上下底面的距离.
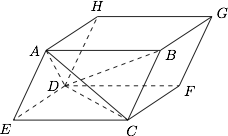 在底面平行四边形 $ECFD$ 中,$$EC = a,CD = b,\sin \angle DCE = \sin \theta ,$$于是$$\begin{split}{S_{ECFD}} &= 2{S_{\triangle DCE}}\\ &= 2 \cdot \dfrac{1}{2}\sin \theta \cdot ab\\ &= ab\sin \theta ,\end{split}$$所以$${V_{A - BCD}} = \dfrac{1}{6}{V_{ABGH - ECFD}} = \dfrac{1}{6}abd\sin \theta .$$
在底面平行四边形 $ECFD$ 中,$$EC = a,CD = b,\sin \angle DCE = \sin \theta ,$$于是$$\begin{split}{S_{ECFD}} &= 2{S_{\triangle DCE}}\\ &= 2 \cdot \dfrac{1}{2}\sin \theta \cdot ab\\ &= ab\sin \theta ,\end{split}$$所以$${V_{A - BCD}} = \dfrac{1}{6}{V_{ABGH - ECFD}} = \dfrac{1}{6}abd\sin \theta .$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3