已知椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 (a>b>0)$ 的短轴长为 $2\sqrt{3}$,右焦点为 $F(1,0)$,点 $M$ 是椭圆 $C$ 上异于左、右顶点 $A,B$ 的一点.
【难度】
【出处】
无
【标注】
-
求椭圆 $C$ 的方程;标注答案$\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$解析略
-
若直线 $AM$ 与直线 $x=2$ 交于点 $N$,线段 $BN$ 的中点为 $E$.证明:点 $B$ 关于直线 $EF$ 的对称点在直线 $MF$ 上.标注答案略解析如图,作椭圆 $C$ 的右准线 $x=4$,作 $MH$ 垂直右准线 $x=4$ 于点 $H$.设直线 $AM$ 交右准线 $x=4$ 于点 $G$,设直线 $FG$ 交直线 $x=2$ 于点 $E_1$,因为\[
\dfrac{|FA|}{|FM|}=\dfrac{|DA|}{|HM|}=\dfrac{|GA|}{|GM|},
\]所以 $FG$ 是 $\triangle FAM$ 中 $\angle AFM$ 的外角平分线,即 $FG$ 平分 $\angle BFM$.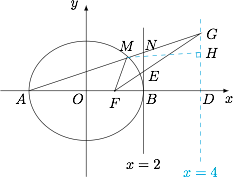 注意到\[
注意到\[
\dfrac{\left|E_1B\right|}{|GD|}=\dfrac{1}{3}, \dfrac{\left|NB\right|}{|GD|}=\dfrac{2}{3},
\]故点 $E_1$ 与点 $E$ 重合,所以 $FE$ 平分 $\angle BFM$,进而点 $B$ 关于直线 $EF$ 的对称点在直线 $MF$ 上.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2