证明：棱长为 $1$ 的正四面体的棱在任一平面上的投影长度的平方之和为定值．
【难度】
【出处】
无
【标注】
【答案】
定值为 $4$
【解析】
先证明
引理 已知非零空间向量 $\overrightarrow a,\overrightarrow b,\overrightarrow c$ 两两垂直，$\overrightarrow m$ 为空间任意非零向量且与 $\overrightarrow a,\overrightarrow b,\overrightarrow c$ 的夹角分别为 $\alpha,\beta,\gamma $，则\[\cos^2\alpha+\cos^2\beta+\cos^2\gamma =1.\]证明 不妨设 $\overrightarrow a,\overrightarrow b,\overrightarrow c,\overrightarrow m$ 均为单位向量，且 $\overrightarrow m=x\overrightarrow a+y\overrightarrow b+z\overrightarrow c$，则\[\cos \alpha=\overrightarrow a\cdot \overrightarrow m=\overrightarrow a\cdot \left(x\overrightarrow a+y\overrightarrow b+z\overrightarrow c\right)=x,\]类似的，有 $\cos\beta=y$，$\cos\gamma =z$，于是\[\cos^2\alpha+\cos^2\beta+\cos^2\gamma=x^2+y^2+z^2=\left|\overrightarrow m\right|^2=1,\]引理得证．
将正四面体 $OABC$ 放入棱长为 $\dfrac{\sqrt 2}2$ 的正方体 $OGAF-EBHC$ 中研究，如图．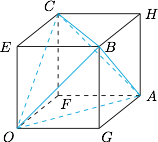
记 $\overrightarrow{OE}=\overrightarrow a$，$\overrightarrow {OF}=\overrightarrow b$，$\overrightarrow{OG}=\overrightarrow c$，$\overrightarrow m$ 为投影面的单位法向量，且与 $\overrightarrow a,\overrightarrow b,\overrightarrow c$ 的夹角分别为 $\alpha,\beta,\gamma $，则所求棱的投影长度的平方和\[\begin{split}M&=\sum_{cyc}\left(OA^2-\left(\overrightarrow {OA}\cdot \overrightarrow m\right)^2\right)+\sum_{cyc}\left(AB^2-\left(\overrightarrow {AB}\cdot \overrightarrow m\right)^2\right)\\
&=6-\sum_{cyc}\left(\left(\overrightarrow b+\overrightarrow c\right)\cdot \overrightarrow m\right)^2-\sum_{cyc}\left(\left(\overrightarrow a-\overrightarrow b\right)\cdot \overrightarrow m\right)^2\\
&=6-\sum_{cyc}\left(\dfrac{\sqrt 2}2\cos\beta+\dfrac{\sqrt 2}2\cos\gamma\right)^2-\sum_{cyc}\left(\dfrac{\sqrt 2}2\cos\alpha-\dfrac{\sqrt 2}2\cos\beta\right)^2\\
&=6-\sum_{cyc}\cos^2\alpha-\sum_{cyc}\cos^2\beta\\
&=4,\end{split}\]为定值，因此原命题得证．
将正四面体 $OABC$ 放入棱长为 $\dfrac{\sqrt 2}2$ 的正方体 $OGAF-EBHC$ 中研究，如图．
记 $\overrightarrow{OE}=\overrightarrow a$，$\overrightarrow {OF}=\overrightarrow b$，$\overrightarrow{OG}=\overrightarrow c$，$\overrightarrow m$ 为投影面的单位法向量，且与 $\overrightarrow a,\overrightarrow b,\overrightarrow c$ 的夹角分别为 $\alpha,\beta,\gamma $，则所求棱的投影长度的平方和\[\begin{split}M&=\sum_{cyc}\left(OA^2-\left(\overrightarrow {OA}\cdot \overrightarrow m\right)^2\right)+\sum_{cyc}\left(AB^2-\left(\overrightarrow {AB}\cdot \overrightarrow m\right)^2\right)\\&=6-\sum_{cyc}\left(\left(\overrightarrow b+\overrightarrow c\right)\cdot \overrightarrow m\right)^2-\sum_{cyc}\left(\left(\overrightarrow a-\overrightarrow b\right)\cdot \overrightarrow m\right)^2\\
&=6-\sum_{cyc}\left(\dfrac{\sqrt 2}2\cos\beta+\dfrac{\sqrt 2}2\cos\gamma\right)^2-\sum_{cyc}\left(\dfrac{\sqrt 2}2\cos\alpha-\dfrac{\sqrt 2}2\cos\beta\right)^2\\
&=6-\sum_{cyc}\cos^2\alpha-\sum_{cyc}\cos^2\beta\\
&=4,\end{split}\]为定值，因此原命题得证．
答案
解析
备注
