椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\left(a>b>0\right)$ 的右焦点 $F\left(c,0\right)$ 关于直线 $y={\dfrac bc}x$ 的对称点 $Q$ 在椭圆上，则椭圆的离心率是 \((\qquad)\)
【难度】
【出处】
2015年高考浙江卷（文）
【标注】
【答案】
B
【解析】
如图，设直线 $QF$ 与直线 $y=\dfrac bcx$ 的交点为 $M$，过 $Q$ 作直线 $y=\dfrac bcx$ 的平行线，交 $x$ 轴于点 $F'$．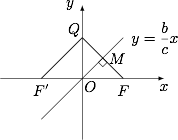
因为 $M$ 平分线段 $QF$，于是 $O$ 平分线段 $F'F$，因此 $F'$ 为椭圆的左焦点．进而由 $F'Q$ 的斜率为 $\dfrac{b}{c}$ 可知 $Q$ 为椭圆的上顶点，因此 $\triangle F'QF$ 为等腰直角三角形，进而不难得到 $e=\dfrac{\sqrt 2}2$．
因为 $M$ 平分线段 $QF$，于是 $O$ 平分线段 $F'F$，因此 $F'$ 为椭圆的左焦点．进而由 $F'Q$ 的斜率为 $\dfrac{b}{c}$ 可知 $Q$ 为椭圆的上顶点，因此 $\triangle F'QF$ 为等腰直角三角形，进而不难得到 $e=\dfrac{\sqrt 2}2$．
题目
答案
解析
备注
