某港口 $ O $ 要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口的 $ O $ 北偏西 $ 30^\circ $ 且与该港口相距 $ 20 $ 海里的 $ A $ 处，并正以 $ 30 $ $ 海里{/}小时 $ 的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以 $ v $ $ 海里{/}小时 $ 的航行速度匀速行驶，经过 $ t $ 小时与轮船相遇．
【难度】
【出处】
2010年高考福建卷（文）
【标注】
-
若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？标注答案$30\sqrt 3 $ $ 海里{/}小时 $解析可由余弦定理表达出小艇的航行距离 $ S $，当 $ S $ 最小时求出相应的 $v$ 即可；也可以画出草图，易判断当小艇和轮船的航行方向垂直时，小艇的航行距离最小，再解直角三角形即可．解法一：设相遇时小艇的航行距离为 $ S $ 海里，则\[\begin{split}S&= \sqrt {900{t^2} + 400 - 2 \times 30t \times 20\cos \left({{90}^ \circ} - {{30}^ \circ}\right)} \\&= \sqrt {900{t^2} - 600t + 400} = \sqrt {900{{\left(t - \dfrac{1}{3}\right)}^2} + 300} ,\end{split}\]故 $ t=\dfrac 1 3 $ 时，$S _{\min} =10\sqrt 3 $，$v=\dfrac{10\sqrt 3 }{{\dfrac{1}{3}}} = 30\sqrt 3 $，
即小艇以 $30\sqrt 3 $ $ 海里{/}小时 $ 的速度航行，相遇时小艇的航行距离最小．
解法二：
若相遇时小艇的航行距离最小，又轮船沿正东方向匀速行驶，则小艇航行方向为正北方向．
设小艇与轮船在 $ C $ 处相遇．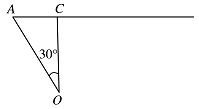
在 ${\mathrm{Rt}}\triangle OAC$ 中，$OC = 20\cos {30^ \circ } = 10\sqrt 3 $，$AC = 20\sin {30^ \circ } = 10$．
又 $AC = 30t$，$OC = vt$，此时，轮船航行时间 $t = \dfrac{10}{30} = \dfrac{1}{3}$，所以\[v = \dfrac{10\sqrt 3 }{{\dfrac{1}{3}}} = 30\sqrt 3 .\]即小艇以 $30\sqrt 3 $ $ 海里{/}小时 $ 的速度行驶，相遇时小艇的航行距离最小． -
为保证小艇在 $ 30 $ 分钟内（含 $ 30 $ 分钟）能与轮船相遇，试确定小艇航行速度的最小值；标注答案$10\sqrt {13} $ $ 海里{/}小时 $解析用草图画出极限位置（动中取静），解三角形，由余弦定理表达出 $v^2$，再配方求解．设小艇与轮船在 $ B $ 处相遇，
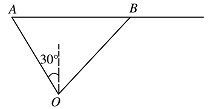由题意可知\[\left(vt\right)^2 =20^2 +\left(30 t\right)^2-2\cdot 20\cdot 30t\cdot \cos \left(90^\circ -30^\circ \right),\]化简得\[v^2=\dfrac{400}{t^2} - \dfrac{600}{t} +900 =400 {\left(\dfrac{1}{t} - \dfrac{3}{4}\right)^2} +675.\]由于 $ 0<t\leqslant \dfrac 1 2 $，即 $ \dfrac 1 t \geqslant 2 $，
所以当 $\dfrac{1}{t} =2$ 时，$v$ 取得最小值 $10\sqrt {13} $，即小艇航行速度的最小值为 $10\sqrt {13} $ $ 海里{/}小时 $． -
是否存在 $ v $，使得小艇以 $ v $ $ 海里{/}小时 $ 的航行速度行驶，总能有两种不同的航行方向与轮船相遇？若存在，试确定 $ v $ 的取值范围；若不存在，请说明理由．标注答案略解析本小题主要考查一元二次方程的实际应用，难点是换元法和主元的选择．由（2）知\[{v^2} = \dfrac{400}{t^2} - \dfrac{600}{t} + 900 ,\]设 $\dfrac{1}{t} = u$ $\left(u > 0\right)$，于是\[400{u^2} - 600u + 900 - {v^2} = 0 . \quad \cdots \cdots ① \]小艇总能有两种不同的航行方向与轮船相遇，等价于方程 $ ① $ 应有两个不等正根，即\[{\begin{cases}
{600^2} - 1600\left(900 - {v^2}\right) > 0, \\
900 - {v^2} > 0. \\
\end{cases}}\]解得\[15\sqrt 3 < v < 30 .\]所以 $v$ 的取值范围是 $\left(15\sqrt 3 ,30\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
