为了解学生身高情况，某校以 $ 10\% $ 的比例对全校 $ 700 $ 名学生按性别进行分层抽样调查，测得身高情况的统计图如下：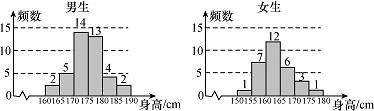
【难度】
【出处】
无
【标注】
-
估计该校男生的人数；标注答案估计该校男生的人数为 $ 400 $ 人．解析看懂统计图表是解决问题的关键．样本中男生人数为 $ 40 $，其占全校学生的比例为 $ 10\% $，可估计全校男生人数为 $ 400 $ 人．
-
估计该校学生身高在 $ 170\sim185 $ $ {\mathrm{cm}} $ 之间的概率；标注答案估计该校学生身高在 $ 170\sim185 $ $ {\mathrm{cm}} $ 之间的概率为 $ 0.5$．解析可以用样本估计总体．由统计图知，样本中身高在 $ 170\sim185 {\mathrm{cm}} $ 之间的学生有 $ 14+13+4+3+1=35 $ 人，
样本容量为 $ 70 $，所以样本中学生身高在 $ 170\sim180 {\mathrm{cm}} $ 之间的概率 $ p_1=\dfrac {35} {70} =0.5 $．故估计该校学生身高在 $ 170\sim185 $ $ {\mathrm{cm}} $ 之间的概率为 $ 0.5$． -
从样本中身高在 $ 180\sim190 $ $ {\mathrm{cm}} $ 之间的男生中任选 $ 2 $ 人，求至少有 $ 1 $ 人身高在 $ 185\sim190 $ $ {\mathrm{cm}} $ 之间的概率．标注答案所求概率为 $\dfrac{3}{5}$．解析考查古典概型．样本中身高在 $ 180\sim185 $ $ {\mathrm{cm }}$ 之间的男生有 $ 4 $ 人，设其编号为 ①，②，③，④，
样本中身高在 $ 185\sim190 $ $ {\mathrm{cm}} $ 之间的男生有 $ 2 $ 人，设其编号为 ⑤，⑥，
从上述 $ 6 $ 人中任取 $ 2 $ 人的树状图为：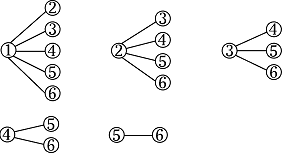
故从样本中身高在 $ 180\sim190 $ $ {\mathrm{cm}} $ 之间的男生中任选 $ 2 $ 人的所有可能结果数为 $ 15 $，
至少有 $ 1 $ 人身高在 $ 185\sim190 $ $ {\mathrm{cm }}$ 之间的可能结果数为 $ 9 $，因此所求概率 ${p_2} = \dfrac{9}{15} = \dfrac{3}{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
