题目 有 $ 7 $ 位歌手（$ 1 $ 至 $ 7 $ 号）参加一场歌唱比赛，由 $ 500 $ 名大众评委现场投票决定歌手名次．根据年龄将大众评委分为五组，各组的人数如下：\[ \begin{array}{|c|c|c|c|c|c|} \hline<br/>组别 & A & B & C & D & E \\ \hline<br/>人数 & 50 & 100 & 150 & 150 & 50 \\ \hline<br/>\end{array} \] 问题1 为了调查评委对 $ 7 $ 位歌手的支持情况，现用分层抽样方法从各组中抽取若干评委，其中从 $B$ 组抽取了 $ 6 $ 人，请将其余各组抽取的人数填入下表．\[ \begin{array}{|c|c|c|c|c|c|} \hline<br/>组别 & A & B & C & D & E \\ \hline<br/>人数 & 50 & 100 & 150 & 150 & 50 \\ \hline<br/>抽取人数 & & 6 & & & \\ \hline<br/>\end{array} \] 答案1 \[\begin{array}{|c|c|c|c|c|c|} \hline<br/>组别 & A & B & C & D & E \\ \hline<br/>人数 & 50 & 100 & 150 & 150 & 50 \\ \hline<br/>抽取人数 & 3 & 6 & 9 & 9 & 3 \\ \hline<br/>\end{array}\] 解析1 本题考查分层抽样．各层抽取的人数均成比例．由题设知，分层抽样的抽取比例为 $6\% $，所以各组抽取的人数如下表：\[\begin{array}{|c|c|c|c|c|c|} \hline<br/>组别 & A & B & C & D & E \\ \hline<br/>人数 & 50 & 100 & 150 & 150 & 50 \\ \hline<br/>抽取人数 & 3 & 6 & 9 & 9 & 3 \\ \hline<br/>\end{array}\] 备注1 问题2 在（1）中，若 $A,B$ 两组被抽到的评委中各有 $ 2 $ 人支持 $ 1 $ 号歌手，现从这两组被抽到的评委中分别任选 $ 1 $ 人，求这 $ 2 $ 人都支持 $ 1 $ 号歌手的概率． 答案2 $\dfrac 29$． 解析2 本题考查古典概型，求出基本事件空间和满足题意的事件个数即可．记从 $A$ 组抽到的 $ 3 $ 位评委分别为 ${a_1},{a_2},{a_3}$，其中 ${a_1},{a_2}$ 支持 $ 1 $ 号歌手；<br/>从 $B$ 组抽到的 $ 6 $ 位评委分别为 ${b_1},{b_2},{b_3},{b_4},{b_5},{b_6}$，其中 ${b_1},{b_2}$ 支持 $ 1 $ 号歌手，<br/>从 $\left\{ {{a_1},{a_2},{a_3}} \right\}$ 和 $\left\{ {{b_1},{b_2},{b_3},{b_4},{b_5},{b_6}} \right\}$ 中各抽取 $ 1 $ 人的所有结果如图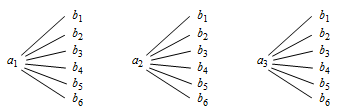：<img src="/static/images/ee20a64288235e6faf0831930d16fe19.png" class="img-responsive" />由树状图知所有结果共 $ 18 $ 种，其中 $ 2 $ 人都支持 $ 1 $ 号歌手的有 ${a_1}{b_1},{a_1}{b_2},{a_2}{b_1},{a_2}{b_2}$ 共 $ 4 $ 种，故所求概率为\[p = \dfrac{4}{18} = \dfrac{2}{9}.\] 备注2