$\dfrac{x^2}{4} + \dfrac{y^2}{3} = 1$

本题考查轨迹方程的求法．直接设动点坐标，根据题意建立等式关系，化简即可．如图 ①，设点 $M$ 到直线 $l$ 的距离为 $d$，根据题意，\[d = 2 \left|MN \right|,\] 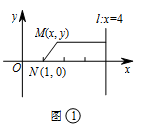由此得\[\left|4 - x \right| = 2\sqrt {{{\left(x - 1\right)}^2} + {y^2}},\]化简得\[\dfrac{x^2}{4} + \dfrac{y^2}{3} = 1,\]所以动点 $M$ 的轨迹 $C$ 的方程为\[\dfrac{x^2}{4} + \dfrac{y^2}{3} = 1.\]

$ - \dfrac{3}{2}$ 或 $\dfrac{3}{2}$

本题的核心在于条件“$A$ 是 $PB$ 的中点”的转化，根据图中点的位置关系，可将上述条件转化为“点 $B$ 的横坐标是点 $A$ 的横坐标的 $2$ 倍”．方法一：
由题意，设直线 $m$ 的方程为 $y = kx + 3$，$A\left({x_1},{y_1}\right)$，$B\left({x_2},{y_2}\right)$，如图 ②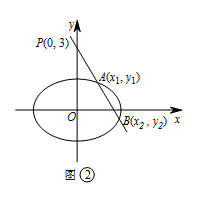． 将 $y = kx + 3$ 代入 $\dfrac{x^2}{4} + \dfrac{y^2}{3} = 1$ 中，有\[\left(3 + 4{k^2}\right){x^2} + 24kx + 24 = 0,\]其中，\[\begin{split}\Delta &= {\left(24k\right)^2} - 4 \times 24\left(3 + 4{k^2}\right) \\&= 96\left(2{k^2} - 3\right) \\&> 0,\end{split}\]即 $k^2>\dfrac 32$．
由根与系数的关系，得\[\begin{split}{x_1} + {x_2} &= -\dfrac{24k}{{3 + 4{k^2}}}, \quad \cdots \cdots ① \\ {x_1}{x_2} &= \dfrac{24}{{3 + 4{k^2}}}, \quad \cdots \cdots ② \end{split}\]又 $A$ 是 $PB$ 的中点，故 ${x_2} = 2{x_1}, \quad \cdots \cdots ③ $
将 ③ 代入 ①②，得\[{x_1} = - \dfrac{8k}{{3 + 4{k^2}}},x_1^2 = \dfrac{12}{{3 + 4{k^2}}},\]可得\[{\left( {\dfrac{ - 8k}{{3 + 4{k^2}}}} \right)^2} = \dfrac{12}{{3 + 4{k^2}}},\]且 ${k^2} > \dfrac{3}{2}$，解得\[k = - \dfrac{3}{2} 或 k = \dfrac{3}{2},\]所以直线 $m$ 的斜率为 $ - \dfrac{3}{2}$ 或 $\dfrac{3}{2}$．
方法二：
设 $A\left({x_1},{y_1}\right)$，$B\left({x_2},{y_2}\right)$．
因为 $A$ 是 $PB$ 的中点，所以\[{x_1} = \dfrac{x_2}{2} , \quad \cdots \cdots ① \\ {y_1} = \dfrac{{3 + {y_2}}}{2} \quad \cdots \cdots ② \]又\[\dfrac{x_1^2}{4} + \dfrac{y_1^2}{3} = 1, \quad \cdots \cdots ③ \\ \dfrac{x_2^2}{4} + \dfrac{y_2^2}{3} = 1 , \quad \cdots \cdots ④ \]联立 ①②③④，解得\[{\begin{cases}
{x_2} = 2, \\
{y_2} = 0, \\
\end{cases}}或{\begin{cases}{x_2} = - 2, \\
{y_2} = 0, \\
\end{cases}}\]即点 $B$ 的坐标为 $\left(2,0\right)$ 或 $\left( - 2,0\right)$，所以直线 $m$ 的斜率为 $ - \dfrac{3}{2}$ 或 $\dfrac{3}{2}$．