如图，三角形 $PDC$ 所在的平面与长方形 $ABCD$ 所在的平面垂直，$PD=PC=4$，$AB=6$，$BC=3$．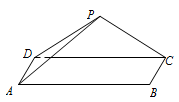
【难度】
【出处】
2015年高考广东卷（文）
【标注】
-
求证：$BC\parallel 平面 PDA$；标注答案略解析本小问考查的是线面平行，证明线面平行的关键是在平面中找到一条线与已知直线平行即可．因为四边形 $ABCD$ 为长方形，
所以 $ BC\parallel AD$．
又 $BC\not\subset 平面PDA$，$AD\subset 平面PDA$，
所以 $BC\parallel 平面 PDA$． -
证明：$BC\perp PD$；标注答案略解析本小问是证明线线垂直，证明线线垂直一般通过线面垂直来证明，根据题中条件 $BC\perp DC$，故需要证明 $BC$ 垂直于 $PD$ 所在的平面 $PDC$．因为 $ BC\perp CD$，$平面PDC\perp 平面ABCD$ 且 $平面PDC\cap 平面ABCD=CD$，$BC\subset 平面ABCD$，
所以 $ BC\perp 平面PDC$．
因为 $PD\subset 平面 PDC$，所以 $ BC\perp PD$． -
求点 $C$ 到平面 $PDA$ 的距离．标注答案点 $C$ 到平面 $PDA$ 的距离为 $\dfrac{3\sqrt 7}{2}$解析本小问是求点到平面的距离，一般我们可以通过等体积法求出高，即点到平面的距离．
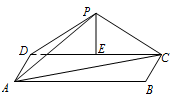取 $CD$ 的中点 $E$，连接 $PE$，$AC$．
因为 $ PD=PC$，所以 $ PE\perp CD$，于是\[ PE=\sqrt{PC^2-CE^2}=\sqrt{4^2-3^2}=\sqrt 7.\]因为 $平面PDC\perp 平面ABCD$ 且 $平面PDC\cap 平面ABCD=CD$，$PE\subset 平面PDC$，
所以 $ PE\perp 平面 ABCD$．
由 $(2)$ 知 $BC\perp 平面PDC$，又 $AD\parallel BC$，
所以 $ AD\perp 平面PDC$．
又 $PD\subset 平面PDC$，所以 $AD\perp PD$．
设点 $C$ 到平面 $PDA$ 的距离为 $h$，则 $V_{C-PDA}=V_{P-ACD}$，所以\[\dfrac 13S_{\triangle PDA}\cdot h=\dfrac 13S_{\triangle ACD}\cdot PE ,\]故\[ h=\dfrac{S_{\triangle ACD}\cdot PE}{S_{\triangle PDA}}=\dfrac{\dfrac 12\times 3\times 6\times \sqrt 7}{\dfrac 12\times 3\times 4}=\dfrac{3\sqrt 7}{2} ,\]因此，点 $C$ 到平面 $PDA$ 的距离为 $\dfrac{3\sqrt 7}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
