设 $a$ 为实数,函数 $f\left(x\right)=\left(x-a\right)^2+|x-a|-a\left(a-1\right)$.
【难度】
【出处】
无
【标注】
-
若 $f\left(0\right)\leqslant 1$,求 $a$ 的取值范围;标注答案$a$ 的取值范围为 $a\leqslant \dfrac 12$.解析第(1)小问主要是解绝对值不等式,属于基础题.由题意可得\[f\left(0\right)=a^2+{\left|{a}\right|}-a^2+a={\left|{a}\right|}+a\leqslant 1 ,\]当 $a\leqslant 0$ 时,$0\leqslant 1$,成立;
当 $a>0$ 时,$2a\leqslant 1$,得 $a\leqslant \dfrac 12$,即 $0<a\leqslant \dfrac 12$.
综上,$a$ 的取值范围为 $a\leqslant \dfrac 12$. -
讨论 $f\left(x\right)$ 的单调性;标注答案$f\left(x\right)$ 在 $\left[a,+\infty\right)$ 上单调递增,在 $\left(-\infty,a\right)$ 上单调递减.解析主要考察了函数的单调性,函数 $f(x)$ 是含绝对值的函数,一般我们先去绝对值,然后再分段考虑单调性.由题意可得\[f\left(x\right)=\begin{cases}x^2-\left(2a-1\right)x,&x\geqslant a,\\ x^2-\left(2a+1\right)x+2a,&x<a,\end{cases}\]当 $x\geqslant a$ 时,$f\left(x\right)$ 对应的抛物线的对称轴为\[x=\dfrac{2a-1}{2}=a-\dfrac 12<a ,\]且开口向上,所以 $ f\left(x\right)$ 在 $\left[a,+\infty\right) $ 上单调递增;
当 $x<a$ 时,$f\left(x\right)$ 对应的抛物线的对称轴为\[x=\dfrac{2a+1}{2}=a+\dfrac 12>a ,\]且开口向上,所以 $ f\left(x\right)$ 在 $\left(-\infty,a\right)$ 上单调递减.
综上,$f\left(x\right)$ 在 $\left[a,+\infty\right)$ 上单调递增,在 $\left(-\infty,a\right)$ 上单调递减. -
当 $a\geqslant 2$ 时,讨论 $f\left(x\right)+\dfrac4x$ 在区间 $\left(0,+\infty\right)$ 内的零点个数.标注答案当 $a=2$ 时,$f\left(x\right)+\dfrac 4x$ 有一个零点 $x=2$;当 $a>2$ 时,$f\left(x\right)+\dfrac 4x$ 有两个零点.解析因为第(2)问是研究函数 $f(x)$ 的单调性,且函数 $y=-\dfrac{4}{x}$ 的性质也比较简单,故研究函数 $f(x)+\dfrac{4}{x}$ 的零点问题,可以将其看成函数 $y=f(x)$ 与函数 $y=-\dfrac{4}{x}$ 的交点问题.由(2)知,$f\left(x\right)_{\min}=f\left(a\right)=a-a^2$.
① 当 $a=2$ 时,$f\left(x\right)_{\min}=f\left(2\right)=-2$,\[f\left(x\right)=\begin{cases}x^2-3x,&x\geqslant 2,\\ x^2-5x+4,&x<2,\end{cases}\]令 $g\left(x\right)=-\dfrac 4x\left(x>0\right)$.
当 $x<2$ 时,$f\left(x\right)=x^2-5x+4$,因为 $ f\left(x\right)$ 在 $\left(0,2\right)$ 上单调递减,所以 $ f\left(x\right)>f\left(2\right)=-2$.
而 $g\left(x\right)=-\dfrac 4x$ 在 $\left(0,2\right)$ 上单调递增,所以 $g\left(x\right)<g\left(2\right)=-2$,所以 $ f\left(x\right)$ 与 $g\left(x\right)$ 在 $\left(0,2\right)$ 上无交点.
当 $x\geqslant 2$ 时,$f\left(x\right)=x^2-3x$,\[f\left(x\right)+\dfrac 4x=0 ,\]即\[x^3-3x^2+4=0 ,\]整理得 $\left(x-2\right)^2\left(x+1\right)=0$.
又 $x\geqslant 2$,所以 $ x=2$.故当 $a=2$ 时,$f\left(x\right)+\dfrac 4x$ 有一个零点 $x=2$.
② 当 $a>2$ 时,\[f\left(x\right)_{\min}=f\left(a\right)=a-a^2<0 .\]当 $x\in\left(0,a\right)$ 时,$f\left(0\right)=2a>4$,$f\left(a\right)=a-a^2$,而 $g\left(x\right)=-\dfrac 4x$ 在 $x\in\left(0,a\right)$ 上单调递增.
当 $x=a$ 时,$g\left(a\right)=-\dfrac 4a$.
又\[a-a^2-\left(-\dfrac 4a\right)=\dfrac{-\left(a-2\right)\left(a^2+a+2\right)}{a}<0 ,\]所以 $ f\left(a\right)=a-a^2<-\dfrac 4a$,如图,易得当 $a>2$ 时,$f\left(x\right)$ 与 $g\left(x\right)=-\dfrac 4x$ 有两个交点.
综上,当 $a=2$ 时,$f\left(x\right)+\dfrac 4x$ 有一个零点 $x=2$;当 $a>2$ 时,$f\left(x\right)+\dfrac 4x$ 有两个零点.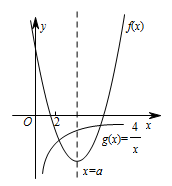
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3