查看数据源：59cca579310996000af46ac1
某网店统计了连续三天售出商品的种类情况：第一天售出 $19$ 种商品，第二天售出 $13$ 种商品，第三天售出 $18$ 种商品；前两天都售出的商品有 $3$ 种，后两天都售出的商品有 $4$ 种，则 \((\qquad)\)
A: 该网店第一天售出但第二天未售出的商品有 $14$ 种
B: 该网店第一天售出但第二天未售出的商品有 $16$ 种
C: 该网店这三天售出的商品最少有 $32$ 种
D: 该网店这三天售出的商品最少有 $29$ 种
【难度】
【出处】
2016年高考北京卷（文）
【标注】
  • 知识点
    >
    函数
    >
    集合与映射
    >
    集合与集合的关系
  • 知识点
    >
    计数与概率
    >
    计数中的常用知识
    >
    容斥原理
【答案】
BD
【解析】
如图，区域 $I,II,III$ 表示只在第一、二、三天售出的商品；区域 $IV,V,VI$ 表示只在第一、二天，第二、三天，第一、三天售出的商品；区域 $VII$ 表示三天都售出的商品．它们的数量分别为 $x_i$（$i=1,2,\cdots ,7$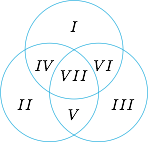）．选项 AB考虑该网店第一天售出但第二天未售出的商品．根据题意，有 $x_1+x_4+x_6+x_7=19$，而 $x_4+x_7=3$，因此 $x_1+x_6=19-3=16$．
选项 CD考虑该网店这三天售出的商品．根据容斥原理，这三天售出的商品总数为$$19+13+18-(3+4+x_6+x_7)+x_7=43-x_6,$$而$$x_5+x_7=4,$$因此$$x_6\leqslant 18-4=14,$$因此这三天售出的商品总数最少有 $29$ 种．
题目 答案 解析 备注
0.115076s