已知过原点的动直线 $l$ 与圆 $C_1:x^2+y^2-6x+5=0$ 相交于不同的两点 $A$，$B$．
【难度】
【出处】
无
【标注】
-
求圆 $C_1$ 的圆心坐标；标注答案圆 $ C_1 $ 的圆心坐标为 $ C_1\left(3,0\right) $．解析考查圆的方程，是基础题．把圆 $ C_1 $ 的一般方程化为标准方程得\[ \left(x-3\right)^2+y^2=4 ,\]所以，圆 $ C_1 $ 的圆心坐标为 $ C_1\left(3,0\right) $．
-
求线段 $AB$ 的中点 $M$ 的轨迹 $C$ 的方程；标注答案点 $ M $ 的轨迹 $ C $ 的方程为 $ x^2-3x+y^2=0 $，其中 $ \dfrac 53<x\leqslant 3 $，其轨迹为一段圆弧．解析根据中点满足的几何性质，用求轨迹方程的直译法求出中点 $M$ 的轨迹方程．求轨迹方程后需要注意满足轨迹方程的点是否都符合题意．设 $ M\left(x,y\right) $，$ A$，$B$ 为过原点的直线 $ l $ 与圆 $ C_1 $ 的交点，且 $ M $ 为 $ AB $ 的中点．故由圆的性质知 $ MC_1\perp MO $，于是\[ \overrightarrow{MC_1}\cdot \overrightarrow{MO}\overset{\left[a\right]}=0.\]（推导中用到：[a]）
又 $ \overrightarrow{MC_1}=\left(3-x,-y\right) $，$ \overrightarrow{MO}=\left(-x,-y\right) $，所以，由向量的数量积的坐标公式得\[ x^2-3x+y^2=0 .\]由题意可知，直线 $ l $ 的斜率存在，所以设直线 $ l $ 的方程为 $ y=mx $，当直线 $ l $ 与圆 $ C_1 $ 相切时，\[ d=\dfrac{{\left|{3m-0}\right|}}{\sqrt{m^2+1}}\overset{\left[b\right]}=2 ,\]（推导中用到：[b]）
解得\[ m=\pm\dfrac{2\sqrt 5}{5} .\]把相切时直线 $ l $ 的方程代入圆 $ C_1 $ 的方程化简得\[9x^2-30x+25=0 ,\]解得 $ x=\dfrac 53 $．
当直线 $ l $ 经过圆 $ C_1 $ 的圆心时，$ M $ 的坐标为 $ \left(3,0\right) $．
又直线 $ l $ 圆 $ C_1 $ 交于 $ A$，$B $ 两点，如图所示，$ M $ 为 $ AB $ 的中点，所以 $\dfrac 53<x\leqslant 3$．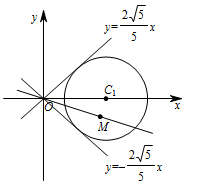
所以点 $ M $ 的轨迹 $ C $ 的方程为 $ x^2-3x+y^2=0 $，其中 $ \dfrac 53<x\leqslant 3 $，其轨迹为一段圆弧． -
是否存在实数 $k$，使得直线 $L:y=k\left(x-4\right)$ 与曲线 $C$ 只有一个交点？若存在，求出 $k$ 的取值范围；若不存在，说明理由．标注答案$k$ 的取值范围是 $-\dfrac{2\sqrt 5}{7}\leqslant k\leqslant \dfrac{2\sqrt 5}{7}$ 或 $k=\pm\dfrac 34$．解析此小问与第（2）问紧密相关，需要用到第（2）问的结果，然后利用数形结合，求出边界，得到取值范围，主要考查直线与圆的位置关系．由题可知，直线 $y=k\left(x-4\right)$ 恒过定点 $A\left(4,0\right)$，结合（2）可作出图象如图所示：
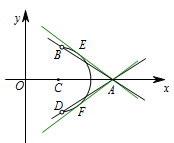由（2）知，点 $B$、$D$ 的横坐标为 $\dfrac53$，因此，代入曲线 $C$ 得 $B\left(\dfrac53,\dfrac{2\sqrt5}{3}\right)$、$D\left(\dfrac53,-\dfrac{2\sqrt5}{3}\right)$，结合图象，可知当 $k$ 介于直线 $AB$ 和 $AD$ 的斜率之间时，直线 $L$ 与曲线 $C$ 只有一个交点，又\[\begin{split}k_{AB}&=\dfrac{\frac{2\sqrt5}{3}-0}{\frac53-4}=-\dfrac{2\sqrt5}{7}, \\k_{AD}&=\dfrac{-\frac{2\sqrt 5}{3}-0}{\frac{5}{3}-4}=\dfrac{2\sqrt5}{7},\end{split}\]所以\[-\dfrac{2\sqrt5}{7}\leqslant k\leqslant \dfrac{2\sqrt5}{7},\]另外，当直线 $L$ 与曲线 $C$ 相切时，只有一个交点，又曲线 $C$ 的圆心为 $\left(\dfrac32,0\right)$，设 $L$ 的直线方程为\[kx-y-4k=0 ,\]所以\[d=\dfrac{|-\frac52k|}{\sqrt{k^2+1}}\overset{\left[c\right]}=\dfrac32,\]（推导中用到：[c]）
解得\[k=\pm\dfrac34 .\]综上所述，$k$ 的取值范围是 $-\dfrac{2\sqrt 5}{7}\leqslant k\leqslant \dfrac{2\sqrt 5}{7}$ 或 $k=\pm\dfrac 34$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
